¹ Universidad de San Martín de Porres, Lima, Perú.

^* Dirección de correspondencia: Sergio Dominguez-Lara. Tomás Marsano 242 (5to piso), Lima 34, Perú. Correos: sdominguezl@usmp.pe, sdominguezmpcs@gmail.com.

Recibido: 15 de septiembre de 2019
Revisado: 20 de septiembre de 2019
Aceptado: 28 de septiembre de 2019
Publicado Online: 28 de septiembre de 2019

Dominguez-Lara, S. (2019). Correlación entre residuales en análisis factorial confirmatorio: una breve guía para su uso e interpretación. Interacciones, 5(3), e207. http://dx.doi.org/10.24016/2019.v5n3.207

INTRODUCCIÓN

En el marco del análisis factorial confirmatorio, la evaluación del ajuste del modelo hace referencia a qué tan compatible es el modelo de medición propuesto con los datos recogidos, y su evaluación estadística se realiza con los indicadores denominados índices de ajuste, tanto absolutos como comparativos. Entre los comparativos, destaca el Comparative Fit Index (CFI) que busca conocer en qué medida el modelo propuesto es mejor que otros, y se esperan valores mayores que .90 para apoyar un ajuste favorable (McDonald, & Ho, 2002);  y entre  los índices de ajuste absolutos, que establecen el grado en que el modelo propuesto reproduce los datos por medio de la discrepancia entre la matriz de covarianza del modelo y de la muestra, destacan el Standardized Root Mean Square Residual (SRMR), esperando valores menores que  .08 (McDonald, & Ho, 2002) para el caso de variables continuas, o el Weighted Root Mean Square Residual (WRMR) para variables categóricas donde valores inferiores a la unidad son aceptables (DiStefano, Liu, Jiang, & Shi, 2018); así como el Root Mean Square Error of Approximation (RMSEA),  que presenta una medida de discrepancia el modelo hipotetizado y la matriz de covarianzas de la población, donde se espera que el límite superior del intervalo de  confianza al 90% sea menor que .10 (West, Taylor, & Wu, 2012). Entonces, interpretados de forma conjunta permiten valorar el modelo. 

Como se puede apreciar (Figura 1), en un modelo confirmatorio, además de la variable latente y las cargas factoriales, cada ítem posee un término de error, comúnmente conocido como residual (e), que representa la influencia de una fuente de error distinta al constructo evaluado, y puede ser atribuible a diferentes aspectos tanto del individuo (algún estado o rasgo; incluso alguna condición física) como del instrumento o la situación de evaluación.

En ese sentido, es posible que, dos o más ítems tengan fuentes de error parecidas, que puede ser debido a redundancia percibida del contenido del ítem (Byrne, 2009), así como su proximidad (Dominguez-Lara, & Merino-Soto, 2017), palabras similares que aparecen en diversos ítems, usos idiosincráticos de una misma palabra (incluso en el mismo país), o un ejemplar de la escala impreso en baja calidad.

Esta fuente de error que compartirían dos o más ítems puede visibilizarse estadísticamente por medio de los índices de modificación (IM; Sörbom, 1989) o de enfoques vinculados a las malas especificaciones (Saris, Satorra, & van der Veld, 2009), que los consideran como casos de infra parametrizaciones de residuales correlacionados, es decir, como un parámetro (la correlación entre residuales) que debe especificarse. Sin embargo, esta especificación debe estar justificada teóricamente y ser interpretada sustantivamente (Jöreskog, 1993), es decir, asignarle un significado teórico al comportamiento estadístico de las variables de estudio. Cabe precisar, que la asociación entre residuales puede depender de la muestra que sea evaluada (ver Figura 1 en Brady, Kneebone, & Bailey, 2019), o incluso del modelo de medición evaluado en una sola muestra (ver Figuras 1 – 3 en Sanders, Morawska, Haslam, Filus, & Fletcher, 2014).

La literatura internacional recomienda examinar, reportar y discutir la magnitud de los IM (Williams, Vandenberg & Edwards, 2009), pero pese a ello la realidad es otra: recientemente se encontró que de 56 manuscrito revisados solo 2 discuten la magnitud de los residuales o IM (Crede, 2018), lo que permite inferir que los investigadores no le brindan importancia. En ese sentido, el presente reporte metodológico tiene como objetivo presentar al lector el modelamiento, manejo e interpretación de los residuales correlacionados en un marco de análisis factorial confirmatorio y malas especificaciones. El lector interesado puede consultar bibliografía complementaria (Brown, 2015; Byrne, 2009; Kline, 2016) a fin de conocer el procedimiento subyacente al modelamiento de residuales correlacionados en diferentes software estadístico.

MÉTODO

Participantes

Se contó con la información procedente de 521 estudiantes (75.8% mujeres; M_edad = 20.768), quienes cursaban entre tercer y octavo ciclo de la carrera de psicología en una universidad privada de Lima Metropolitana.

Instrumento

Para ilustrar esta situación, fueron considerados los datos de la Escala de Florecimiento (EF) de Diener et al. (2010) en su versión peruana (Cassaretto & Martínez, 2017), la cual fue administrada como parte de una investigación de mayor envergadura aprobada por la universidad del autor del trabajo. La EF está conformada por ocho ítems en escalamiento Likert de siete opciones (desde Totalmente en desacuerdo hasta Totalmente de acuerdo) que son influidos predominantemente por un solo constructo (modelo unidimensional; Figura 1).

Análisis de datos

Se realizó un análisis factorial confirmatorio con método WLSMV (Weighted Least Squares Mean and Variance Adjusted) con base en matrices policóricas (debido, fundamentalmente, al carácter asimétrico de la distribución de los ítems). Para valorar el modelo fueron usados el CFI, RMSEA y WRMR; y las malas especificaciones fueron evaluadas con un módulo especializado (Dominguez-Lara & Merino-Soto, 2018). El programa utilizado fue Mplus versión 7 (Muthen & Muthen, 1998-2015).

RESULTADOS Y DISCUSIÓN

Luego de evaluar un modelo unidimensional, los índices de ajuste (CFI, RMSEA y WRMR) fueron contrastados con los puntos de corte aceptados por la literatura internacional, y se halló que si bien algunos obtuvieron magnitudes aceptables (CFI = .976), otros estuvieron en el límite de lo admitido (WRMR = 1.027), o fueron desfavorables (RMSEA = .136 [IC90% .120, .153).

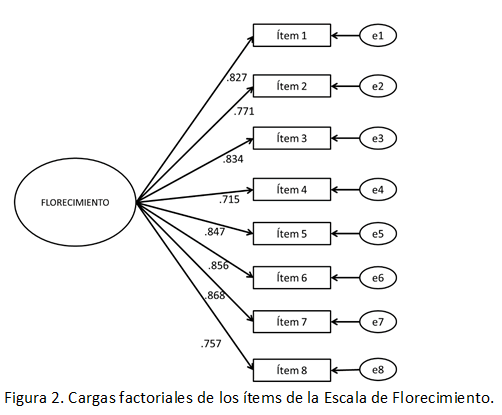
Ello indica que si bien el modelo propuesto es mejor que el modelo en el que las variables son independientes entre sí (CFI), las discrepancias con el modelo hipotetizado aún son importantes (WRMR y RMSEA), aunque las cargas factoriales (Figura 2) fueron aceptables en todos los casos (> .50; Dominguez-Lara, 2018a). Por tal motivo, según la magnitud y significancia de los IM, es necesario incluir en el modelo la correlación entre los residuales de los ítems 6 y 7 (IM = 28.937, p < .001; Cambio estimado en el parámetro = .321) para explicar de forma adecuada el modelo (estadísticamente hablando, para mejorar el ajuste por medio de la disminución del estadístico χ2). 

Sin embargo, como ya se mencionó, para valorar un modelo de medición establecido se parte del supuesto de que la presencia de residuales correlacionados no debería afectar significativamente el ajuste del modelo ni la capacidad explicativa de las variables, es decir, que la relación entre los ítems es capaz de reproducir de forma satisfactoria el modelo original. Por el contrario, los residuales correlacionados modelados permitirían conocer aquellas fuentes de error común a los ítems que pueden ser reducidas (p.e., usar palabras distintas si la fuente de error está basada en el uso frecuente de cierto vocablo) o eliminadas (p.e., ordenar de forma diferente los ítems) en futuras versiones de los instrumentos. Por ejemplo, ¿cómo puede interpretarse el hecho de que los residuales de los ítems 6 y 7 se relacionen? El fraseo de los ítems 6 (Soy una buena persona y vivo una buena vida) y 7 (Soy optimista acerca de mi futuro), además de la palabra inicial (Soy) y la proximidad no tendrían más aspectos en común que expliquen ese la asociación entre residuales.

Con todo, queda una pregunta por responder: ¿la correlación entre residuales aporta sustancialmente al modelo? De forma concreta, si un modelo original (Figura 1) presenta un mal ajuste estadístico, ¿mejorarlo artificialmente por medio del modelamiento de residuales correlacionados ayuda a que sea un mejor modelo desde un punto de vista sustantivo? A modo de ejemplo, fueron implementados de forma consecutiva cinco correlaciones entre residuales (ítems 6 y 7; ítems 2 y 5; ítems 1 y 5; ítems 1 y 4; ítems 6 y 8) que fueron consideradas como potenciales malas especificaciones (Dominguez-Lara & Merino-Soto, 2018).

Una vez realizada esta acción, los índices de ajuste en el modelo re-especificado mejoran de forma marcada (CFI = .992; RMSEA = .090 [IC90% .071, .110]; WRMR = .617); y podrían seguir mejorando conforme se sigan agregando correlaciones entre residuales. Asimismo, al evaluar la diferencia estadística entre el ajuste de ambos modelos con el comando DIFFTEST del Mplus se evidencian diferencias significativas (Δχ2 = 150.039; p < .001): el modelo re-especificado es estadísticamente superior al original.

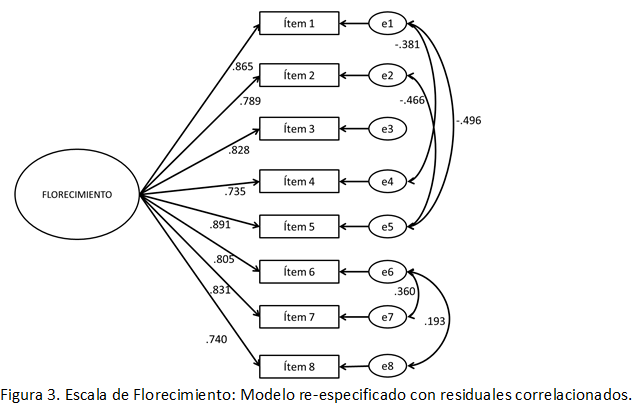
Pese a la mejora estadística, como se aprecia (Figura 3), la influencia del constructo sobre los ítems no cambia de forma significativa respecto al modelo inicial (sin residuales correlacionados), es decir, las cargas factoriales podrían considerarse estadísticamente similares, incluyendo la confiabilidad del constructo antes y después de la re-especificación (coeficiente ω_antes = .934; coeficiente ω_después = .939).

¿Qué hacer frente a la presencia de correlación entre residuales?

Existen ocasiones en las que la especificación de correlación entre residuales puede tener un sustento teórico (Jöreskog, 1993) como en la discusión conceptual de fuentes de error común a dos ítems (Caycho-Rodriguez et al., 2018), así como también metodológico como en la determinación del efecto del método asociado a ítems invertidos (ver Wu, Zuo, Wen, & Yan, 2017; Moreta-Herrera, López-Calle, Ramos-Ramírez, & López-Castro, 2018) o en modelos longitudinales (Green, 2003). Por ese motivo, su uso no puede desestimarse. Por el contrario, implementar correlaciones entre residuales podrían ayudar a identificar oportunidades de mejora para el instrumento, como detectar cuestiones vinculadas al fraseo de los ítems (Dominguez-Lara, Merino-Soto, & Gutiérrez-Torres, 2018; Ventura-León, Jara-Avalos, Garcia-Pajuelo, & Ortiz-Saenz, 2018) o eliminar ítems aparentemente redundantes (Calderón-De la Cruz, Dominguez-Lara, & Arroyo-Rodríguez, 2018; Navarro-Loli & Dominguez-Lara, 2019). Es decir, especificar esos parámetros (residuales correlacionados) puede ayudar, a posteriori, a reducir la dependencia local de los ítems al interior de una escala (Reise, Waller, & Comrey, 2000) por medio de acciones directas.

Entonces, dado que su implementación puede aportar a la valoración psicométrica de un instrumento, hacerlo con el único objetivo demejorar el ajuste (e.g., Haslam, Filus, Morawska, Sanders, & Fletcher, 2015; Moscoso, Merino-Soto, Dominguez-Lara, Chau, & Claux, 2016; Seo & Kwon, 2018) potencialmente contribuiría a sobrevalorar un modelo que podría ser inherentemente inadecuado (por fallas internas, predominantemente), pudiéndose observar casos en los que la cantidad de residuales correlacionados es tan alta, sea 20 (Schaufeli, Bakker, Hoogduin, Schaap, & Kladler, 2001; p. 573; Sullman, Stephens, & Yong, 2015, p. 77) o 17 (Sullman, Stephens, & Kuzu, 2013, p.46) pares de residuales correlacionados, que los resultados obtenidos pueden ser cuestionables.
Esto es relevante porque esos parámetros adicionales no intervienen en la relación de los ítems con la variable latente, en la sumatoria final de los ítems o la interpretación de la puntuación; solo dan la imagen de buen ajuste, pero no aportarían algo sustancial a la interpretación del constructo.

Por otro lado, si es implementado por los motivos inicialmente mencionados (e.g., coherencia teórica) debe efectuarse la corrección de la confiabilidad del constructo en presencia de residuales correlacionados (Dominguez-Lara, 2016; Viladrich, Angulo-Brunet, & Doval, 2017) porque su presencia sesga las estimaciones (Gu, Little, & Kingston, 2013). Por ejemplo, en otros estudios luego de modelar los residuales correlacionados se calculó su potencial impacto en la confiabilidad del constructo y se determinó que fue prácticamente nulo (Calderón-De la Cruz, Lozano, Cantuarias, & Ibarra, 2018; Dominguez-Lara, & De la Cruz-Contreras, 2017), además de no influir sustancialmente en el ajuste estadístico del modelo (Solano & Copez-Lonzoy, 2017). Empero, existen casos en los que es más previsible un decremento, como el de Sullman et al. (2015) donde la dimensión adaptive/constructive alcanza un ω de .88 y disminuye a .79 una vez aplicado el procedimiento de corrección mencionado anteriormente o la dimensión verbal/agressive que baja de .83 a .75; o en Seo y Kwon (2018), que disminuye de .889 a .817; y aunque puede parecer que la disminución no es significativa, en otras ocasiones puede llegar a ser elevada (Fernández-Arata, Juárez-García, & Merino-Soto, 2015; Viladrich et al., 2017).

Hasta aquí, se podría dar la impresión de que se está anteponiendo el método a la teoría, pero no es así. En primer lugar, queda claro que la elección de un marco teórico solvente y con vasta evidencia es uno de los pasos iniciales al momento de construir un instrumento de evaluación psicológica, ya que sobre esa base se elaborarán los ítems (Muñiz & Fonseca-Pedrero, 2019). De ese modo, se prevé que el producto final tenga adecuadas evidencias de validez con relación al contenido de los ítems y que, además, los ítems sean influidos satisfactoriamente por el constructo que evalúan (evidencias de validez con respecto a su estructura interna), y que esa influencia significativa no sea reemplazada (o enmascarada) por otras fuentes de variabilidad. 

En segundo lugar, si se desea dar credibilidad a los hallazgos psicológicos, es necesario partir de mediciones con sólidas y suficientes evidencias de validez y confiabilidad. En ese sentido, los argumentos previos ayudan a reforzar la idea de que la relación de los ítems  con el constructo debe ser aquello que brinde fortaleza al modelo, no elementos ajenos que, por el contrario, disminuyen la validez de las inferencias. En otros trabajos (Dominguez-Lara, 2018b; Bonifay, Lane, & Reise, 2017) se ha hecho énfasis en la necesidad de unificar la teoría con criterios metodológicos sólidos para lograr hallazgos que tengan mayor credibilidad. 

Conclusiones

El problema de la inclusión de residuales correlacionados para mejorar el ajuste estadístico en un modelo de medición no es nuevo, pero en vista del uso indiscriminado del método es necesario llamar la atención sobre ello.

Si bien es un procedimiento cuestionable, es una práctica ampliamente difundida y respaldada por algunos investigadores a lo largo del tiempo (e.g., Haslam et al, 2015; Seo, & Kwon, 2018; Sullman et al., 2013), aunque existen reportes que evitan esta práctica (e.g., Loera, Converso, & Viotti, 2014). No obstante, en base a lo expuesto podría concluirse que su implementación no implica necesariamente mejoras en la comprensión sustantiva del modelo y eleva de forma espuria los índices de ajuste (Dunn, Baguley, & Brunsden, 2014), pudiendo orientar de forma errada al investigador al momento de plasmar sus conclusiones. Inclusive, llevaría al investigador novel a seleccionar instrumentos de evaluación psicológica que no cumple con criterios de calidad suficientes, o a perpetuar la práctica de este procedimiento bajo la creencia errada de si lo hace la mayoría, debe estar bien (argumentum ad populum) sin un análisis de sus implicancias en medición, más aún cuando existe evidencia de que su discusión es un tópico prácticamente ignorado en las publicaciones (Crede, 2018).

Finalmente, un argumento se asemeja al canto de sirena cuando es un discurso aparentemente convincente, pero que de un modo u otro esconde algún tipo de engaño o manipulación de la realidad; y como se puede apreciar, la psicometría no es ajena a ello. Por esto, se aconseja un uso racional del procedimiento, de preferencia cuando su inclusión tenga un carácter técnico o metodológico.

CONFLICTO DE INTERÉS

El autor declara que no existen conflictos de interés en la elaboración del manuscrito.

FINANCIAMIENTO

El presente estudio recibió financiamiento parcial por parte de la Universidad de San Martín de Porres.

REFERENCIAS

Bonifay, W., Lane, S.P., & Reise, S.P. (2017). Three concerns with applying a bifactor model as a structure of psychopathology. Clinical Psychological Science, 5(1), 184 – 186.  doi: 10.1177/2167702616657069

Brady, B., Kneebone, I. I., & Bailey, P. E. (2019). Validation of the Emotion Regulation Questionnaire in older community‐dwelling adults. British Journal of Clinical Psychology, 58(1), 110-122. doi:10.1111/bjc.12203

Brown, T. (2015). Confirmatory Factor Analysis for Applied Research (2nd Ed.). New York: The Guilford Press.

Byrne, B. M. (2009). Structural equation modeling with AMOS: Basic concepts, applications, and programming. New York, NY: Routledge & Taylor & Francis.

Calderón-De la Cruz, G., Dominguez-Lara, S., & Arroyo-Rodríguez, F. (2018). Análisis psicométrico preliminar de una medida breve de autoeficacia profesional en trabajadores peruanos: AU-10. Psicogente, 21(39), 12-24. doi: 10.17081/psico.21.39.2819

Calderón-De la Cruz, G., Lozano, F., Cantuarias, A., & Ibarra, L. (2018). Validación de la Escala Satisfacción con la Vida en trabajadores peruanos. Liberabit, 24(2), 249-264. doi: 10.24265/liberabit.2018. v24n2.06

Cassaretto, M., & Martínez, P. (2017). Validación de las escalas de bienestar, de florecimiento y afectividad. Pensamiento Psicológico, 15(1), 19-31. Recuperado a partir de //revistas.javerianacali.edu.co/index.php/pensamientopsicologico/article/view/1255

Caycho-Rodríguez, T., Ventura-León, J., Noe-Grijalva, M., Barboza-Palomino, M., Arias, W., Reyes-Bossio, M., & Rojas-Jara, C. (2018). Evidencias psicométricas iniciales de una medida breve sobre preocupación por el cáncer. Psicooncología, 15(2), 315-325. doi: 10.5209/PSIC.61438

Crede, M. (2018). Questionable research practices when using confirmatory factor analysis. Journal of Managerial Psychology, 34(1), 18-30. doi: 10.1108/JMP-06-2018-0272

Diener, E., Wirtz, D., Tov, W., Kim-Prieto, C., Choi, D., Oishi, S. & Biswas-Diener, R. (2010). New Well-Being  Measures:  Short  Scales  to  Assess  Flourishing and Positive and Negative Feelings. Social  Indicators  Research, 97(2),  143-156.  doi: 10.1007/s11205-009-9493-y

DiStefano, C., Liu, J., Jiang, N., & Shi, D. (2018). Examination of the weighted root mean square residual: Evidence for trustworthiness? Structural Equation Modeling, 25(3), 453-466. Doi: 10.1080/10705511.2017.1390394

Dominguez-Lara, S. (2016). Errores correlacionados y estimación de la fiabilidad en estudios de validación: comentarios al trabajo validación de la escala ehealth literacy (eheals) en población universitaria española. Revista Española de Salud Pública, 90(9), e1-e2. Recuperado desde: http://scielo.isciii.es/pdf/resp/v90/1135-5727-resp-90-e60002.pdf

Dominguez-Lara, S. (2018a). Propuesta de puntos de corte para cargas factoriales: una perspectiva de fiabilidad de constructo. Enfermería Clínica, 28(6), 401. doi: 10.1016/j.enfcli.2018.06.002

Dominguez-Lara, S. (2018b). Sobre carretas, caballos, y otras cuestiones psicométricas. Interacciones, 4(3), 199-200. doi: 10.24016/2017.v4n3.152

Dominguez-Lara, S. & De la Cruz-Contreras, F. (2017). Análisis estructural y desarrollo de una versión breve de la versión en español del Inventario de Ansiedad ante Exámenes (TAI-E) en universitarios de Lima. Interacciones, 3(1), 7-17. doi: 10.24016/2017.v3n1.50

Dominguez-Lara, S. & Merino-Soto, C. (2017). Una modificación del coeficiente alfa de Cronbach por errores correlacionados. Revista Médica de Chile, 145, 269-274. Doi: 10.4067/S003498872017000200018.

Dominguez-Lara, S., & Merino-Soto, C. (2018). Evaluación de las malas especificaciones en modelos de ecuaciones estructurales. Revista Argentina de Ciencias del Comportamiento, 10(2), 19 – 24. doi: 10.32348/1852.4206.v10.n2.19595

Dominguez-Lara, Merino-Soto y Gutiérrez-Torres (2018). Estudio Estructural de una Medida Breve de Inteligencia Emocional en Adultos: El EQ-i-M20. Revista Iberoamericana de Diagnóstico y Evaluación – e Avaliação Psicológica, 49(4), 5-21. doi: 10.21865/RIDEP49.4.01

Dunn, T. J., Baguley, T. & Brunsden, V. (2014). From alpha to omega: A practical solution to the pervasive problem of internal consistency estimation. British Journal of Psychology, 105(3), 399-412. doi: 10.1111/bjop.12046

Fernández-Arata, M., Juárez-García, A., & Merino-Soto, C. (2015). Análisis estructural e invarianza de medición del MBI-GS en trabajadores peruanos. Liberabit, 21(1), 9-20. Recuperado de http://www.scielo.org.pe/scielo.php?script=sci_arttext&pid=S1729-48272015000100002&lng=es&tlng=es.

Gu, F., Little, T. D., & Kingston, N. M. (2013). Misestimation of reliability using coefficient alpha and structural equation modeling when assumptions of tau-equivalence and uncorrelated errors are violated. Methodology, 9(1), 30–40. doi:10.1027/1614-2241/a000052

Green, S.B. (2003). A coefficient alpha for test-retest data. Psychological Methods, 8(1), 88–101. doi: 10.1037/1082-989X.8.1.88

Haslam, D., Filus, A., Morawska, A., Sanders, M. R., & Fletcher, R. (2015). The Work–Family Conflict Scale (WAFCS): Development and initial validation of a self-report measure of work–family conflict for use with parents. Child Psychiatry & Human Development, 46(3), 346-357. doi: 10.1007/s10578-014-0476-0

Jöreskog, K. G. (1993). Testing structural equation models. 294–316 in: Bollen, K. A. and Long, J. S. (eds.) Testing Structural Equation Models. Beverly Hills: Sage.

Kline, R.B. (2016). Principles and practice of structural equation modeling. New York: The Guilford Press.

Loera, B., Converso, D., & Viotti, S. (2014) Evaluating the Psychometric Properties of the Maslach Burnout Inventory-Human Services Survey (MBI-HSS) among Italian Nurses: How Many Factors Must a Researcher Consider? PLoS ONE, 9(12): e114987. doi:10. 1371/journal.pone.0114987  

McDonald, R.P., & Ho, M..H. R. (2002). Principles and practice in reporting structural equation analyses. Psychological Methods, 7, 64–82. doi: 10.1037/1082-989X.7.1.64

Moreta-Herrera, R., López-Calle, C., Ramos-Ramírez, M. & López-Castro, J. (2018). Estructura factorial y fiabilidad del Cuestionario de Salud General de Goldberg (GHQ-12) en universitarios ecuatorianos. Revista Argentina de Ciencias del Comportamiento, 10(3), 35-42. doi: 10.32348/1852.4206.v10.n3.20405

Moscoso, M.S., Merino-Soto, C., Dominguez-Lara, S., Chau, C.B., & Claux, M. (2016). Análisis factorial confirmatorio del inventario multicultural de la expresión de la ira y hostilidad. Liberabit, 22(2), 137-152. Recuperado de http://www.scielo.org.pe/scielo.php?script=sci_arttext&pid=S1729-48272016000200002&lng=es&tlng=es.

Muñiz, J., & Fonseca-Pedrero, E. (2019). Diez pasos para la construcción de un test. Psicothema, 31(1), 7 - 16. doi: 10.7334/psicothema2018.291

Muthén, L.K., & Muthén, B.O. (1998-2015). Mplus User’s guide (7th ed.). Los Angeles, CA: Muthén & Muthén.

Navarro-Loli, J.S., & Dominguez-Lara, S. (2019). Propiedades psicométricas de la Escala de Autoeficacia Percibida Específica de Situaciones Académicas en adolescentes peruanos. Psychology, Society, & Education, 11(1), 53-68. doi: 10.25115/psye.v10i1.1985

Reise, S. P., Waller, N. G., & Comrey, A. L. (2000). Factor analysis and scale revision. Psychological Assesment, 12, 287-297. doi:10.1037/1040-3590.12.3.287

Sanders, M. R., Morawska, A., Haslam, D. M., Filus, A., & Fletcher, R. (2014). Parenting and Family Adjustment Scales (PAFAS): validation of a brief parent-report measure for use in assessment of parenting skills and family relationships. Child Psychiatry & Human Development, 45(3), 255-272. doi: 10.1007/s10578-013-0397-3

Saris, W.E, Satorra, A., & van der Veld, W.M. (2009). Testing structural equation modeling or detection of misspecifications? Structural Equation Modeling, 16, 561 – 582. doi: 10.1080/10705510903203433

Schaufeli, W. B., Bakker, A. B., Hoogduin, K., Schaap, C., & Kladler, A. (2001). On the clinical validity of the Maslach Burnout Inventory and the Burnout Measure. Psychology & Health, 16(5), 565-582. doi: 10.1080/08870440108405527.

Seo, J. W., & Kwon, S. M. (2018). Preliminary Validation of a Korean Version of the Acquired Capability for Suicide Scale‐Fearlessness About Death. Suicide and Life‐Threatening Behavior, 48(3), 305-314. doi: 10.1111/sltb.12360

Solano, C. & Copez-Lonzoy, A. (2017). Análisis preliminar del cuestionario señales de alerta de recaída (AWARE) en drogodependientes peruanos. Interacciones, 3(2), 87-94. doi: 10.24016/2017.v3n2.65

Sörbom, D. (1989). Model modification. Psychometrika, 54(3), 371-384. doi: 10.1007/BF02294623

Sullman, M.J.M, Stephens, A.N., & Kuzu D. (2013). The expression of anger amongst Turkish taxi drivers. Accident Analysis and Prevention, 56, 42  50. doi: 10.1016/j.aap.2013.03.013

Sullman, M.J.M., Stephens, A.N., & Yong, M. (2015). Anger, aggression and road rage behaviour in Malaysian drivers. Transportation Research Part F: Traffic Psychology and Behaviour, 29, 70 – 82. doi: 10.1016/j.trf.2015.01.006

Ventura-León, J., Jara-Avalos, S., Garcia-Pajuelo, C., & Ortiz-Saenz, C. (2018). Validación de una escala de perfeccionismo en niños peruanos. Actualidades en Psicología, 32(124), 16-33. Recuperado de https://www.scielo.sa.cr/pdf/ap/v32n124/2215-3535-ap-32-124-16.pdf

Viladrich, C., Angulo-Brunet, A., & Doval, E. (2017). A journey around alpha and omega to estimate internal consistency reliability. Anales de Psicología, 33(3), 755-782. doi: 10.6018/analesps.33.3.268401

West, S.G., Taylor, A.B., & Wu, W. (2012). Model fit and model selection in structural equation modeling. In R. H. Hoyle (Ed.), Handbook of Structural Equation Modeling (pp. 209–231). New York, NY: Guilford

Williams, L. J., Vandenberg, R. J., & Edwards, J.R. (2009). Structural equation modeling in management research: A guide for improved analysis. Academy of Management Annals, 3, 543-604. doi: 10.1080/19416520903065683

Wu, Y., Zuo, B., Wen, F., & Yan, L. (2017). Rosenberg Self-Esteem Scale: Method effects, factorial structure and scale invariance across migrant child and urban child populations in China. Journal of Personality Assessment, 99(1), 83-93. doi: 10.1080/00223891.2016.1217420