http://dx.doi.org/10.24016/2018.v4n3.134

ARTÍCULOS ORIGINALES

Variación de la escala Likert en el test de utilidad de la matemática

Variation in Likert scale of the mathematics usefulness test

Facundo Juan Pablo Abal^1,2*, Sofía Esmeralda Auné^1,2 y Horacio Félix Attorresi²

CITARLO COMO:

RESUMEN

El objetivo de este trabajo es comparar los resultados obtenidos en estudios de validez y confiabilidad de una Escala de Utilidad de la Matemática cuando varían los formatos Likert de los ítems. El test mide las creencias de estudiantes de Psicología respecto de la importancia atribuida a la Matemática para la carrera y el futuro desarrollo profesional. Participaron 939 estudiantes de Psicología (81% mujeres) quienes respondieron a los ítems usando escalas de 3, 5 y 6 categorías. Se controló el efecto del orden de exposición de los individuos a cada formato y se incluyeron además otros instrumentos para reducir la memorización de las respuestas. Las escalas Likert con más categorías incrementaron la precisión del instrumento en los niveles extremos del rasgo, pero a costa de comprometer las evidencias sobre la estructura interna (Análisis Factorial Confirmatorio y Modelo de Crédito Parcial de la Teoría de Respuesta al ítem). La función de eficiencia relativa reveló que se obtiene similar información para todos los niveles del rasgo usando 5 y 6 opciones. La cantidad de categorías Likert no afectó sustantivamente la relación de la Utilidad con otras variables.

PALABRAS CLAVE

ABSTRACT

The aim of this work was to compare the results obtained in validity and reliability studies of a mathematics usefulness scale when the Likert format of the items varies. The test measured beliefs about the importance attributed to mathematics for career progress and future professional development. The 939 Psychology students (81% female) who participated responded to the items using 3, 5 and 6 categories. The effect of the order of exposure of individuals to each format was controlled and other tests were also included to reduce answer memorization. Likert scales with more categories increased test reliability at the extreme levels of the trait, but at the expense of compromising the internal structure validity evidences (Confirmatory Factor Analysis and Partial Credit Model of the Item Response Theory). The relative efficiency function revealed that similar information is obtained for all levels of the trait when using 5 or 6-point scales. The number of Likert categories did not substantially affect the relationship between usefulness and other variables.

KEY WORDS

Psychological tests; psychometrics; mathematics education; university students.

El formato de respuesta de ítems pertenecientes a tests de comportamiento típico es una decisión crucial que debe tomar quien construye el instrumento. Aun cuando se reconoce la importancia del diseño cuidadoso que debería seguirse, es poco frecuente que los autores expliciten por qué utilizan una cantidad de respuestas específica o por qué escogen determinados cuantificadores lingüísticos para acompañar a las opciones. Se suele invertir mucho esfuerzo en realizar un análisis minucioso de las frases que operacionalizan el indicador pero existe una tendencia bastante generalizada a desatender su formato de respuesta (Wetzel & Greiff, 2018). Así ha ganado fama el formato habitual de cinco opciones con anclajes lingüísticos que reflejan distintos grados de acuerdo con las frases. Sin embargo, las razones argumentadas para elegir este formato parecen estar más influidas por la tradición y el pragmatismo que por fundamentos psicométricos (Bisquerra, & Pérez-Escoda, 2015; Muñiz, García-Cueto & Lozano, 2005).

El estudio de la cantidad óptima de opciones de respuesta para las escalas tipo Likert es un tema de larga data sobre el que todavía hay muchos interrogantes abiertos. Symonds (1924) inauguró el debate respecto de la cantidad de opciones necesarias para garantizar un mínimo valor aceptable de confiabilidad inter-jueces. Desde de entonces, se han llevado adelante numerosas investigaciones tanto empíricas (e.g. Abal, Auné, Lozzia & Attorresi, 2017; Alwin, Baumgartner, & Beattie, 2018; Finn, Ben-Porath & Tellegen, 2015; González-Betanzos, Leenen, Lira-Mandujano & Vega-Valero, 2012; Nunes et al, 2008; Toland & Usher, 2016) como con simulación (e.g. Culpepper, 2013; Lee, & Paek, 2014; Lozano, García-Cueto & Muñiz, 2008; Muñiz, et al., 2005) que analizaron los efectos de variar la escala de respuesta a los ítems sobre la confiabilidad y las evidencias internas y externas de validez. Pero la gran variabilidad de los resultados imposibilita concluir la existencia de ese número mágico pretendido por Cox (1980). Los investigadores han recomendado formatos de respuesta que van desde dos o tres opciones (Matell & Jacoby, 1971, Sancerni, Meliá & González, 1990) hasta escalas con 24 (Champney & Marshall, 1939) o 101 opciones (Bandura, 2006).

Una forma de interpretar la diversidad de los hallazgos conlleva suponer que no existe un principio general para describir la relación de la cantidad de opciones de respuesta con los indicadores de validez y confiabilidad. En efecto, los resultados de algunos investigadores ayudan a defender cierta estabilidad en las propiedades psicométricas de la prueba con independencia del formato de respuesta (e.g. Jones & Loe, 2013; Matell & Jacoby, 1971; Wakita, Ueshima & Noguchi, 2012). Desde una perspectiva teórica, Muñiz et al. (2005) entienden que si la modificación de la escala Likert alterara sustancialmente los resultados de la medición de una variable habría que revisar aspectos de la validez de constructo.

La inconsistencia de los resultados también podría responder a que el número óptimo de opciones se halla supeditado a las características propias del constructo o al instrumento diseñado para su medición. En este sentido, Guilford (1954) defendió la idea de que el formato de respuesta debiera estudiarse empíricamente para cada situación. No obstante, en la actualidad se entiende que podría resultar arduo, costoso y poco práctico (Morales, 2006).

Una de las principales razones que dificultan la comparación de los hallazgos reportados en los estudios es el énfasis puesto a los diversos criterios usados para establecer qué es un comportamiento óptimo de la escala (validez, confiabilidad o discriminación de los ítems). A esto debe sumarse una dimensión diacrónica, en la medida en que estos criterios fueron definidos y analizados de diferente forma en cada etapa de la evolución histórica de la psicometría (González-Betanzos et al., 2012; Kramp, 2006). Por ejemplo, el fuerte cuestionamiento que ha recibido el supuesto de continuidad de la escala en el análisis de formatos tipo Likert ha derivado en nuevos lineamientos para el tratamiento estadístico de datos en estudios de fiabilidad (e.g. Elosua & Zumbo, 2008) y de validez factorial (e.g. Lloret-Segura, Ferreres-Traver, Hernández-Baeza & Tomás-Marco, 2014).

La Psicometría se ha perfeccionado ofreciendo actualmente teorías, modelos y métodos más sofisticados. En las últimas décadas el desarrollo creciente de la Teoría de Respuesta al Ítem (TRI) introdujo un conjunto de estrategias metodológicas para profundizar en el estudio de la optimización de las escalas Likert. Estas investigaciones han analizado el número de opciones que maximizan la función de información del test y que mejoran los indicadores de ajuste al modelo. En términos generales, la mayoría tiende a ubicar entre tres y siete la cantidad óptima de categorías (Lozano et al., 2008; Nunes et al., 2008; Toland & Usher, 2016) aunque podría variar en función del modelo de la TRI aplicado y la dimensionalidad de los datos (Hernández et al., 2000) o la longitud del test y la capacidad discriminativa de los ítems (Lee & Paek, 2014). La discrepancia más importante aparece al intentar establecer si un aumento en el número de opciones mejora (González-Betanzos et al, 2012; Hernández, Muñiz, & García-Cueto, 2000) o perjudica (Kramp, 2006; Lee & Paek, 2014; Maydeu-Olivares, Kramp, García-Forero, Gallardo-Pujol & Coffman, 2009) a las evidencias internas de validez analizadas a partir del ajuste al modelo de la TRI.

Como es posible apreciar, a pesar de los esfuerzos, los hallazgos no son concluyentes y parecen indicar que no es posible encontrar un formato superior a otro en términos universales (Hernández et al., 2000; Morales, 2006). En este trabajo se busca realizar un aporte al estudio del efecto que produce la variación de la cantidad de opciones de respuesta de los ítems sobre las propiedades psicométricas de un test. Dado que se propone un estudio empírico, se comparan los resultados obtenidos en una prueba específica que mide la Utilidad de la Matemática para estudiantes de Psicología (Abal, Galibert, Aguerri & Attorresi, 2014). Este constructo permite evaluar un conjunto de creencias acerca de la importancia y aplicabilidad que el estudiante de dicha carrera le atribuye a la Matemática tanto para sus estudios (utilidad presente) como para el ejercicio profesional (utilidad futura). Existe un acuerdo bastante extendido para la inclusión de la Utilidad dentro de las variables fundamentales de la dimensión afectiva de la enseñanza de la Matemática (Martínez, 2008; McLeod & McLeod, 2002). Además, este constructo presenta una larga tradición en el marco del estudio de la estructura de las actitudes hacia la matemática, en donde ha sido denominado como Valor (Tapia & Marsh, 2004), Aplicabilidad (Bazán & Sotero, 1998) y Utilidad (Adelson & McCoach 2011; Auzmendi, 1992; Fennema & Sherman, 1976; Palacios, Arias & Arias, 2014).

A la luz de estas consideraciones teóricas y metodológicas, se plantea como objetivo general de este trabajo analizar cómo repercute sobre las propiedades psicométricas del test de Utilidad emplear formatos de respuesta tipo Likert de tres, cinco y seis categorías. En virtud de los criterios registrados en la literatura se ha considerado examinar los efectos de la variación de la cantidad de categorías de respuesta en función de:

1) el ajuste de los datos al Modelo Crédito Parcial de la TRI (MCP, Masters, 2016).

2) las evidencias de validez basadas en la relación entre el constructo Utilidad con otras variables externas.

3) los estudios de confiabilidad clásicos y con TRI.

MÉTODO

Diseño

La investigación realizada responde a las características de un estudio instrumental conforme a la clasificación de diseños de investigación en Psicología de Ato, López y Benavente (2013). Se trata de un desarrollo de corte psicométrico centrado en analizar empíricamente los cambios que se producen en las evidencias de validez y confiabilidad al modificar la cantidad de opciones de respuesta en la escala Likert del instrumento.

Participantes

Participaron 939 alumnos (81% género femenino) que cursan el segundo año de la carrera de Psicología en la Universidad de Buenos Aires. Se trata de una universidad de gestión pública a la que asisten estudiantes con nivel socio económico predominantemente medio y menores proporciones de nivel medio bajo y nivel medio alto. Se utilizó un muestreo no probabilístico por accesibilidad.

Todos los participantes residen en el área metropolitana de Buenos Aires, Argentina. Los alumnos cursan las materias en tres turnos: mañana (34.2%), tarde (28.9%) y noche (36.9%). La edad tuvo un promedio de 22.7 años (DE = 6.3) y varió entre 18 y 59 años sin registrar diferencias significativas en función del género, t(937) = 0.48, p = .63. El 17.3% de los alumnos tiene 25 años o más, por lo que podrían definirse como estudiantes universitarios no tradicionales según el criterio simple basado en la edad (MacDonald, 2018). El 65% reportó dedicarse exclusivamente a las actividades académicas mientras que el resto manifestó combinarlas con un empleo. En cuanto al estado civil, la mayoría de los estudiantes (78%) consignaron ser solteros.

En lo que refiere al rendimiento de los estudiantes en la materia Matemática (correspondiente al primer año de la carrera) se observó una calificación promedio de 6.75 (DE = 1.84). No se observaron diferencias significativa en esta variable en función del género del alumno, t(937)= -1.37, p = .17. El 25% de los estudiantes debió recursar al menos una vez esta materia luego de haber obtenido una calificación desaprobatoria. La condición de recursante de Matemática no se asoció ni con el género χ2(1, N = 939) = 0.18, p = .67, ni con el turno al que asisten los alumnos, χ2(2, N = 939) = 1.35, p = .51.

Instrumentos

Escala de Utilidad de la Matemática. La escala consta de ocho ítems con respuesta tipo Likert de seis opciones: Totalmente en desacuerdo, En desacuerdo, Más bien en desacuerdo, Más bien de acuerdo, De acuerdo y Totalmente de acuerdo. Fue diseñada y validada para población de estudiantes de Psicología dado que los contenidos de los ítems hacen mención explícita a la aplicación de nociones matemáticas en esta carrera.Los estudios psicométricos realizados originalmente sobre este instrumento reportan evidencias de validez basadas en la estructura interna del constructo (Abal, et al., 2014): se corroboró su unidimensionalidad mediante un análisis factorial exploratorio y se ajustó satisfactoriamente el Modelo de Respuesta Graduada de la TRI. Además se informó un índice de consistencia alfa Cronbach de .89 como estimación de la confiabilidad. Los indicadores de calidad psicométrica obtenidos con los datos de la presente investigación son mostrados en los resultados.

Las administraciones se llevaron adelante en grupos reducidos y fueron coordinadas por los autores. Se efectuaron durante la tercera clase de un curso cuatrimestral con frecuencia semanal en el que se dictan contenidos de Psicoestadística (perteneciente al segundo año de la carrera). Aunque el plan de estudios de la carrera incluye a la asignatura Matemática en el primer año, en esta materia no se contempla una articulación ni aplicación a contenidos psicológicos. Por consiguiente, se consideró que en la tercera semana de Psicoestadística los alumnos tienen una aproximación de cómo es posible emplear algunos conceptos de matemática a datos propios de la psicología. Esta aproximación es somera pero suficiente como para responder las creencias de utilidad que indaga la escala analizada en este estudio.

Los estudiantes completaron el protocolo en un formato de lápiz y papel. Previa administración se les explicitó que la tarea consistía en la respuesta a una serie de inventarios que perseguían evaluar cómo se vinculaban los estudiantes de Psicología con la Matemática. Se enfatizó que no había respuestas correctas o incorrectas a las preguntas y que se buscaba sinceridad y compromiso al contestar.

Se les advirtió que podrían encontrar preguntas repetidas pero se aclaró que la finalidad de la investigación no era evaluar su memoria sino su reacción ante los enunciados. La necesidad de incluir esta aclaración en la consigna se desprendió como conclusión de los estudios piloto realizados para la validación aparente de las versiones del protocolo. Allí se encontró que, en ausencia de esta advertencia, los evaluados que detectaban ítems repetidos tendían a revisar las respuestas dadas con los formatos anteriores o mostraban reacciones de fastidio, suspicacia y/o desconcierto. Estos comportamientos fueron infrecuentes durante la administración definitiva del protocolo y neutralizados por los coordinadores.

Las condiciones de su participación fueron explicitadas por escrito en un consentimiento, el cual debieron firmar antes de responder el protocolo. Allí se informó sobre el carácter voluntario de su participación y la posibilidad de abandonar la evaluación en cualquier momento de la actividad. También se les comunicó sobre las garantías de anonimato y confidencialidad de sus respuestas. La colaboración de los sujetos no tuvo ningún tipo de consecuencia ni compensación.

Análisis de los datos

Control de calidad de los datos. La muestra original contaba con 953 casos pero se apartaron 14 usando dos criterios de exclusión: a) protocolos con respuesta aquiescente en por lo menos uno de los instrumentos psicométricos (2 casos) y b) al menos dos ítems omitidos o con doble respuesta en alguna de las escalas administradas (12 casos). Para los protocolos que presentaban datos perdidos pero que no cumplían con los criterios de exclusión mencionados (23 casos) se aplicó un método de imputación basado en el promedio de respuestas obtenidas en ese ítem por el total de los sujetos (Hair, Black, Babin, & Anderson, 2009). No se registraron omisiones en las preguntas centrales indagadas mediante la encuesta de datos sociodemográficos y académicos, por lo que no debió recurrirse a ningún método de sustitución de los datos perdidos con este instrumento.

Unidimensionalidad. Se estudió la unidimensionalidad del constructo Utilidad para cada uno de los formatos Likert aplicando un Análisis Factorial Confirmatorio con el programa Mplus (Muthén & Muthén, 2010). Se estimaron los parámetros con el método de mínimos cuadrados ponderados robustos (Weighted Least Squares Mean and Variance Adjusted, WLSMV) a partir de las matrices de correlaciones policóricas. El método de estimación se escogió respetando el carácter ordinal de los datos obtenidos mediante las escalas Likert. El ajuste al modelo se examinó usando el índice de ajuste comparativo CFI, el índice de Tucker-Lewis (TLI), el error medio cuadrático de aproximación (RMSEA) y la raíz del promedio de los residuos al cuadrado (RMSR).

Estimación y Ajuste del MCP. El MCP fue desarrollado por Masters (1982, 2016) como una extensión del modelo dicotómico Rasch (1960) para su aplicación a ítems con respuesta ordenada. Rasch utilizó una función logística para determinar la probabilidad que tiene un sujeto con un nivel de rasgo θ de puntuar 1 (elegir la opción clave) en el ítem dicotómico i:

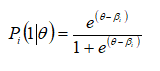
Según la expresión matemática del modelo, esta probabilidad de puntuar 1 en lugar de 0 dependerá de si el evaluado cuenta con un nivel de rasgo θ suficiente como para superar un parámetro de localización βi que caracteriza al ítem. Este parámetro se mide en la misma escala que el rasgo y suele denominarse, en el contexto de los tests de rendimiento típico como parámetro de adhesión (Rojas & Pérez, 2001).

La formulación del MCP se basa en una segmentación adyacente del dato politómico en una serie de dicotomías. De esta manera, frente a un ítem i de m+1 respuestas ordenadas, el modelo permite calcular la probabilidad condicional de responder a la opción h (h = 0,…, m) en lugar de responder a la inmediatamente anterior (h – 1) para todo nivel del rasgo θ. Al igual que en el modelo de Rasch, el paso de una categoría a otra dependerá de la localización un parámetro de adhesión. Sin embargo, en el MCP será necesario definir tantos parámetros βih (umbrales de adhesión) como transiciones presente el ítem politómico de una categoría a otra. Como es lógico suponer, este parámetro se define solamente para las categorías h = 1,…, m porque no existe una categoría anterior a h = 0 y, como consecuencia, tampoco existe el umbral βi0. Es por esta razón que para analizar la escala Likert con tres opciones de respuesta será necesario estimar sólo dos parámetros de umbal βih, para la escala con cinco opciones se requerirán cuatro parámetros βih y para la escala de seis opciones se obtendrán cinco parámetros βih.

La ecuación formal del MCP establece la probabilidad que tiene un individuo con rasgo θ de elegir h en el ítem i según:

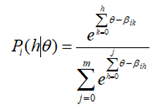Donde se define:

Aunque la expresión resulta matemáticamente compleja, Embretson y Reise (2000) la resumen considerando que la probabilidad de elegir la opción h se define como una exponencial correspondiente a esa opción que se divide por la sumatoria de las exponenciales de todas las categorías del ítem. En esencia, el MCP establece que la probabilidad de una persona de responder la opción h se corresponde con la diferencia entre su nivel de rasgo θ y el conjunto de todos los parámetros de umbral βih del ítem i (Gempp, et al., 2006).

En el marco de la TRI se han desarrollado numerosos modelos, como el Modelo de Respuesta Graduada (Samejima, 2016) o el Modelo de Ratings Scale (Andrich, 2016), que podrían ser tan apropiados como el MCP para el análisis de ítems politómicos. No existe un lineamiento rígido que guíe la elección de uno por sobre otro. No obstante, siguiendo a Penfield (2014), es posible justificar la aplicación del MCP en este estudio considerando tres factores que responden a argumentos teóricos, metodológicos y empíricos. A nivel teórico, es posible suponer que los parámetros ofrecidos por el MCP sirven para representar el proceso de respuesta de un sujeto a un ítem con escala Likert (Masters & Wright, 1997). Al respecto, si bien se propuso inicialmente para modelizar la puntuación de conocimiento parcial en ítems de pruebas de habilidades, la aplicación del MCP a pruebas de rendimiento típico también es destacable (e.g. Abal, Lozzia, Auné & Attorresi, 2017; DiStefano, Morgan & Motl, 2012; Rojas & Pérez, 2001; Shea, Tennant & Pallant, 2009; Smith, Fallowfield, Stark, Velikova, & Jenkins, 2010; Vendramini, Silva & Dias, 2009; Willse, 2017; Zanini & Peixoto, 2016). Desde una mirada metodológica, el tamaño muestral utilizado en la presente investigación responde de manera adecuada a los requerimientos del MCP. Por último, el tercer factor empírico mencionado por Penfield se vincula a la evaluación del ajuste del MCP a los datos recolectados. Estas evidencias forman parte de los resultados de la presente investigación.

La aplicación del MCP se efectuó por separado a los tres formatos Likert operando con el programa Winsteps versión 3.63.0. Se estimaron los parámetros del MCP correspondientes a los ítems y a los sujetos por el Método de Máxima Verosimilitud Conjunta. El ajuste del modelo a los datos obtenidos a partir de cada formato se estudió a nivel global considerando los valores de los estadísticos ajuste próximo (infit) y lejano (outfit). Los infit y outfit se interpretan como medias cuadráticas de los residuales no estandarizados (Mean-Square, MNSQ) y adoptan un valor de 1 cuando se observa un ajuste perfecto entre los datos y el modelo. Linacre (2012) definió una zona de ajuste aceptable y productivo para la medida que se ubica en el intervalo de 0.5 a 1.5 tanto para los infit y outfit de los sujetos y de los ítems. Estos puntos de corte han sido sugeridos por Wright, Linacre, Gustafson, & Martin-Lof (1994) a partir de su importante experiencia en el análisis de datos psicométricos y como resultado de estudios de simulación informales.

Medidas de precisión. En el marco de la teoría clásica de test se estimó la confiabilidad a partir del coeficiente alfa de Cronbach y su intervalo de confianza del 95% para cada uno de los tres formatos de respuesta (Domínguez-Lara & Merino-Soto, 2015). Considerando que existe abundante bibliografía psicométrica que demuestra los sesgos que introduce este coeficiente ante la violación de supuestos tales como la tau-equivalencia de los ítems o la presencia de correlación de los errores (e.g. DeVellis, 2017; Dunn, Baguley, & Brunsden, 2014) se ha decidido ampliar el estudio de la consistencia interna con otros indicadores. Una de las exigencias más importantes del alfa de Cronbach, y que presenta un fuerte impacto para los fines de este trabajo, es el supuesto de continuidad de la escala de respuesta de los ítems. El alfa de Cronbach tiende a infraestimar la consistencia interna cuando se aplica en ítems con pocas opciones (Lozano et al., 2008; Weng, 2004) por lo que resulta necesario recurrir a coeficientes que consideren la naturaleza ordinal de los datos para poder realizar comparaciones más justas entre los diferentes formatos. Con base en estos reparos se calcularon el glb recomendado por Sijtsma (2009) y las versiones ordinales de los coeficientes alfa y omega (Gadermann, Guhn, & Zumbo, 2012; Elosua & Zumbo, 2008). Al igual que con el alfa de Cronbach, también se construyeron IC del 95% para los coeficientes omega ordinal y alfa ordinal con la técnica de boostrap usando el método de sesgo corregido y acelerado (BCa; Kelley & Pornprasertmanit, 2016). Todos los coeficientes de consistencia interna usados se calcularon con el programa R utilizando la función scaleReliability del paquete userfriendlyscience (Peters, 2014).

Desde la perspectiva de la TRI se utilizaron las Funciones de Eficiencia Relativa (ER) obtenidas a partir del cociente de las Funciones de información del test con un formato respecto a otro formato para todo nivel de θ. La ventaja de aplicar las funciones de ER es que estas curvas permiten estimar el aporte de información que realiza un formato Likert con respecto a otro en todo el rango de valores de la variable.

Asociación con otras variables. Se analizaron las asociaciones de los θ estimados según el MCP para cada sujeto a partir de los tres formatos Likert con un conjunto de variables usadas como criterios externos. Se utilizaron pruebas t para la diferencia de medias para estudiar la relación con criterios dicotómicos: género (mujeres vs. varones) y cursantes vs. recursantes de la materia Matemática. Se usó el mismo análisis con la variable edad, que fue dicotomizada según el criterio etario de MacDonald (2018) en estudiantes tradicionales (18 a 24 años) y no tradicionales (25 años o más). Para cuantificar el tamaño del efecto de la diferencia entre los grupos, se calculó la d de Cohen (y su respectivo IC al 95%) con R mediante el comando ci.smd del paquete MBESS (Kelley, 2007). Previamente se verificó el cumplimiento de las condiciones de homocedasticidad (Prueba de Levene) y normalidad dado que d no es robusta ante el incumplimiento de estos supuestos (Coe & Merino-Soto, 2003). La normalidad de las distribuciones se analizó con la prueba de Shapiro-Wilk y se agregaron los coeficientes de asimetría y curtosis de Fisher para considerar la sensibilidad de esta prueba frente a tamaños muestrales grandes (Ghasemi & Zahedias, 2012). Se supuso una aproximación aceptable a la normalidad cuando ambos coeficientes presentaron valores entre ±1 (George & Mallery, 2016). Posteriormente, se compararon los d obtenidos para cada formato. Siguiendo a Kramp (2006) se asumió que no había diferencia significativa si la d que se obtuvo para un formato cayó dentro de los intervalos de confianza correspondientes a los otros formatos.

La asociación entre los θ estimados con cada escala Likert y los criterios medidos cuantitativamente (Afecto, Confianza y calificación en Matemática) se estudió con el índice de correlación r de Pearson. Los r obtenidos con los tres formatos para un mismo criterio externo se compararon usando el intervalo de confianza de la diferencia de dos correlaciones para muestras dependientes con una variable en común. La hipótesis de igualdad de las correlaciones se rechazó si el 95% IC incluía el valor cero (Zou, 2007). Este análisis se efectuó operando el programa cocor (Diedenhofen & Musch, 2015).

RESULTADOS

Supuesto de unidimensionalidad

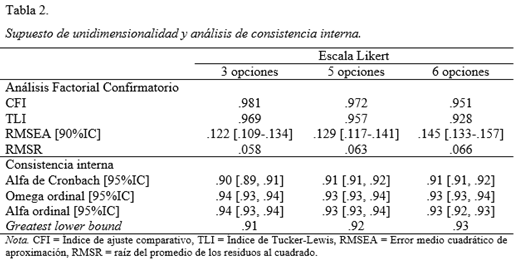
La tabla 2 muestra los índices de ajuste obtenidos en los análisis factoriales confirmatorios realizados para los tres formatos de respuesta. Los resultados reflejan un ajuste al modelo unidimensional aceptable (TLI y CFI > .90) aunque los índices de RMSEA superiores a .08 indican cierto desajuste. Los valores de RMSR calculados sobre los elementos de las matrices de correlaciones policóricas muestran que los residuos fueron relativamente bajos.

Comparación de estimación y ajuste del MCP

La estimación de los parámetros para los tres formatos Likert alcanzó el criterio de convergencia empleando una cantidad razonable de iteraciones. Se estimaron 16 parámetros de umbral para el formato de tres opciones, 32 parámetros para el formato de cinco opciones y 40 parámetros para el formato de seis opciones. Así también se estimaron tres valores de rasgo θ para cada sujeto extraídos sobre la base de sus patrones de respuestas a la prueba con los distintos formatos Likert. No se reportaron inversiones en los parámetros de localización estimados en la modelización de ninguno de los formatos. Esto constituye una importante propiedad de las escalas en tanto que garantiza que las opciones de respuestas de todos los ítems (categorías que presente la escala Likert) son útiles, sin importar la cantidad, para discriminar en algún rango específico de la variable.

Se aplicó un ANOVA de una vía para comparar los θ promedio estimados a partir de las seis diferentes versiones contrabalanceadas del protocolo en las que los formatos se presentaban en distinto orden. No se registraron diferencias estadísticamente significativas para las escalas con tres (F(5,933) = 1.84, p = .103) cinco (F(5,933) = 1.39, p=.226) y seis opciones (F(5,933) = 1.62, p = .153).

Las asociaciones entre los θ estimados para los diferentes formatos de respuesta fueron relativamente altas. El r más elevado se registró entre los formatos de cinco y seis categorías, (r5-6 = .88, p<.0001). En cambio, las asociaciones entre los formatos de tres y cinco opciones, (r3-5 =.80, p<.0001) y la de tres y seis opciones (r3-6 = .78, p<.0001) resultaron más bajas. Para realizar una comparación objetiva de estas correlaciones se calcularon los IC del 95% de la diferencia de dos para muestras dependientes con una variable en común. El IC para r5-6 - r3-6 fue [.079, .123], para la diferencia r5-6 – r3-5 fue [.060, .102] y, finalmente, para r3-5 – r3-6 fue [.018, .039]. Ninguno de los IC incluyó el valor cero evidenciando que las tres diferencias resultaron estadísticamente significativas. Estos resultados reflejan que el número de opciones puede incidir en la medición del constructo justificando los análisis subsiguientes para determinar su impacto en las propiedades psicométricas.

En la tabla 3 se exhiben los índices para la evaluación global del ajuste del modelo a los datos de los tres formatos. Con respecto a los ítems, se observa que para los tres formatos el modelo ajusta razonablemente dado que las medias de los infit y outfit MNSQ han sido próximas a 1. Aun así, cuando la escala Likert presenta seis opciones de respuesta los valores máximos de MNSQ del infit (1.54) y outfit (1.63) se ubican ligeramente por fuera del rango aceptable (0.5 - 1.5) evidenciando cierto desajuste bajo esta condición.

El ajuste de los individuos también se mostró globalmente aceptable con valores medios de los estadísticos infit y outfit cercanos a 1 (tabla 3). Los valores mínimos y máximos de los MNSQ muestran que para los tres formatos existen patrones de respuesta de las personas que presentan desajuste y, por ende, no pueden ser explicados por el MCP. La aparición de un porcentaje reducido de patrones de respuesta anómalos podría resultar aceptable en la medida en que los estadísticos de ajuste resultan sensibles al tamaño muestral grande. No obstante, cabe destacar que se registra un aumento en las desviaciones estándares de estos indicadores a medida que crece la cantidad de opciones del ítem. Esto implica que el modelo pierde capacidad explicativa de una mayor cantidad de patrones de respuestas; lo que se refleja en una mayor cantidad de sujetos que adoptan valores inadecuados de infit y outfit.

A fin de alcanzar mayor capacidad descriptiva se inspeccionaron los valores infit y outfit de cada sujeto. Para la escala Likert de seis opciones los porcentajes de sujetos por fuera del intervalo de ajuste aceptable según Linacre (2012) son de 20.2% y 19.8% para infit y outfit respectivamente. Estos porcentajes de sujetos con patrones desajustados disminuyen a 16.7% y 17.3% cuando se aplica una escala de cinco categorías y a 14.3% y 13.4% si la escala Likert tiene tres opciones.

Medidas de precisión

Los indicadores globales de consistencia interna mostraron índices altamente satisfactorios para los diferentes formatos de escala Likert sin evidenciar diferencias considerables entre ellos (tabla 2).

La figura 1 muestra la Eficiencia Relativa de los diversos formatos de respuesta en función de niveles de θ. La función de ER del formato de seis categorías respecto del de cinco categorías (ER6/5) se mantuvo relativamente constante y próximo a 1 a lo largo de todo el espectro del rasgo latente indicando que ambas pruebas producen la misma información. Los valores de información entre las tres funciones resultaron similares en los valores centrales del rasgo. No obstante, en los extremos del rasgo los formatos de cinco y seis categorías proporcionaron mayor información que cuando se utilizaron tres categorías.

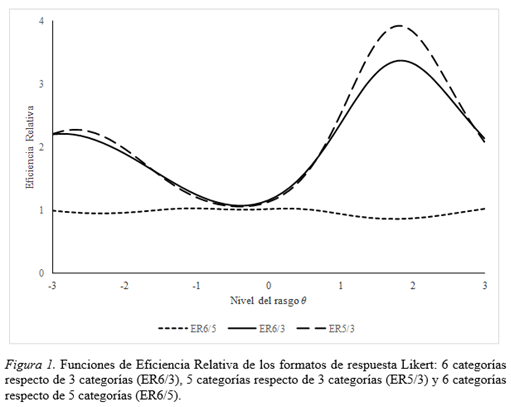
Relación con otras variables

Los resultados obtenidos al considerar la relación de cada formato de respuesta con los criterios externos dicotómicos (género y cursada de Matemática) o dicotomizados (edad) aparecen en la tabla 4. Se verifican condiciones aceptables para la interpretación del tamaño del efecto d dado que se corroboran los supuestos de homocedasticidad y normalidad. Para las submuestras de tamaño grande en las que las pruebas de Shapiro-Wilk rechazan la normalidad de la distribución se observan coeficientes de asimetría y curtosis con valores absolutos inferiores a 1. Con los tres criterios externos usados se observa que los d calculados para un formato Likert se ubicaron dentro de los ICs de los d obtenidos bajo los otros dos formatos.

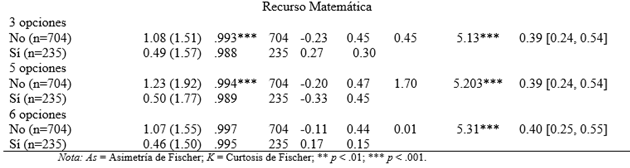
Los análisis efectuados para estudiar la relación de cada formato con criterios externos cuantitativos se exhiben en la tabla 5. En este caso, la comparación de los r para las diferentes escalas Likert se efectuó con un análisis más riguroso que el aplicado con los criterios dicotómicos en virtud de que existe un procedimiento más objetivo. Considerando los intervalos de confianza de la diferencia de dos r puede concluir que no se registran diferencias significativas en las correlaciones de los tres formatos con la calificación obtenida en Matemática. En cambio, las correlaciones del formato de tres opciones con las variables Afecto y Confianza fueron más débiles que las obtenidas con los θ estimados a partir de las escalas de cinco y seis categorías.

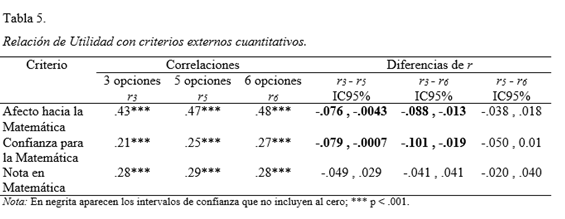
DISCUSIÓN

Los estudios que buscan encontrar el diseño óptimo para el formato de respuesta de los ítems tienen una extensa historia en el campo de la psicometría. No obstante, a pesar de que se han considerado una multiplicidad de opiniones y abordajes metodológicos, el debate sigue abierto (Joshi, Kale, Chandel, & Pal, 2015; Matas, 2018). El objetivo de este trabajo fue estudiar el impacto de la manipulación del formato de respuesta de los ítems sobre las propiedades psicométricas de la escala de Utilidad de la matemática. Para tal fin, se aplicó un diseño metodológico que contempló los efectos intra-individuales en la respuesta de los mismos ítems bajo los tres formatos de respuesta ensayados. Este diseño se contrapone con el propuesto en estudios de simulación, los cuales ofrecen lineamientos generales para el diseño de la escala de respuesta de los ítems. Como señala Kramp (2006), el análisis de datos simulados no considera el proceso psicológico subyacente involucrado en la respuesta a los ítems de un test en particular. Por ende, deben ser tomados con precaución dado que requieren de una contrastación empírica. Es por esta razón que no han perdido vigencia los estudios empíricos que realizan ensayos con diferentes formatos a fin de optimizar la medición (e.g. Alwin, et al., 2018; Finn et al, 2015; Toland & Usher, 2016).

El procedimiento aplicado en este estudio también debe ser diferenciado del utilizado en otros estudios empíricos tales como: a) administrar un único formato y posteriormente reagrupar los datos (e.g. Matell & Jacoby, 1971; Nunes et al., 2008) o b) comparar los resultados obtenidos en la administración de los formatos en muestras independientes (e.g. Adelson & McCoach, 2010; Alwin, et al., 2018; Preston & Colman, 2000). Al igual que lo señalado por otros investigadores (González-Betanzos et al., 2012; Kramp, 2006; Maydeu-Olivares et al., 2009), se considera que la estrategia aquí implementada muestra resultados de mayor calidad y precisión porque permite analizar estrictamente la reacción del individuo frente a las diferentes cantidades de opciones y los anclajes lingüísticos de las escalas comparadas.

La comparación de las correlaciones realizadas entre los θ obtenidos a partir de los diferentes formatos de respuesta dejó en evidencia que la disminución del número de opciones repercute en la estimación de los parámetros de los individuos. En la misma línea, las Funciones de Eficiencia Relativa revelaron que los tres formatos de respuesta alcanzan similar precisión en niveles centrales del rasgo. Sin embargo, las escalas de cinco y seis opciones proporcionan mayor información que la de tres categorías para niveles extremos de Utilidad. Cabe destacar que esta disminución en la precisión de la medida no fue registrada al utilizar los indicadores globales como alfa de Cronbach, omega ordinal, alfa ordinal o glb.

La cantidad de categorías Likert afectó sustantivamente a las evidencias internas de validez. La modelización con TRI reveló que el ajuste global de los datos al modelo unidimensional tendió a mejorar para formatos con menor cantidad de categorías (tres y cinco opciones). Los resultados aquí obtenidos son consistentes con los reportados por otros autores (Kramp, 2006; Lee & Paek, 2014; Maydeu-Olivares et al., 2009) pero se contraponen con los hallazgos de otros estudios (González-Betanzos et al., 2012; Hernández et al., 2000); los cuales reflejaron que las mejoras en el ajuste surgen cuando aumenta el número de opciones.

Por el contrario, el efecto de la variación del formato de respuesta sobre las evidencias externas de validez no resultó tan apreciable como el observado para las evidencias internas. Sólo se registraron diferencias significativas en dos criterios externos medidos cuantitativamente que presentaban características teóricas y tecnológicas similares a Utilidad, como son los constructos Afecto y Confianza. Para los criterios externos dicotómicos y la calificación en Matemática la incidencia de la escala Likert no fue significativa. Con respecto a este punto tampoco se observan resultados concluyentes en la literatura (e.g. González-Betanzos et al., 2012; Kramp, 2006; Maydeu-Olivares et al., 2009; Sancerini, Meliá, & González-Romá, 1990) aunque la falta acuerdo entre estos trabajos podría deberse principalmente a particularidades inherentes a los criterios externos considerados.

En resumen, los formatos con mayor número de categorías incrementaron la precisión del instrumento en los niveles extremos del rasgo, pero a costa de comprometer el ajuste global del modelo. Por el contrario, el formato de tres categorías mejora el ajuste del modelo pero aporta una menor información para medir en una parte considerable del espectro del rasgo. En suma, y en consonancia con las conclusiones de Maydeu-Olivares et al. (2009), la decisión respecto de cuál es la cantidad óptima de opciones de respuesta para la prueba de Utilidad de la Matemática requiere establecer un equilibrio entre el grado de ajuste del modelo y la precisión de la medida. Por lo expuesto, considerando los formatos ensayados, parece conveniente adoptar la escala de cinco categorías.

En cuanto a las limitaciones del presente estudio en el plano metodológico y que obligan a tomar recaudos sobre la generalización de las conclusiones se encuentran la homogeneidad de la muestra considerada y el uso de un muestreo no aleatorio. Con respecto a esto, futuros estudios perseguirán replicar estos resultados aplicando el mismo diseño en grupos con una representación más balanceada de las características socioeducativas.

Un aspecto para destacar es que las conclusiones obtenidas con respecto al número óptimo de categorías de la escala Likert se limitan a la escala de Utilidad de la Matemática y se circunscribe a los formatos que fueron comparados. Si bien estos aspectos reducen las posibilidades de generalización de los resultados, podrían interpretarse como orientadores para la elaboración de otras escalas que midan constructos similares o que indaguen en una población con características análogas. El mayor inconveniente que se presenta en la decisión sobre la cantidad de opciones en la escala Likert es que debe tomarse en una fase inicial de diseño del instrumento. En esta etapa de la construcción del test el elaborador puede no contar con información empírica concreta sobre cómo resultará psicométricamente la prueba. Sin embargo, podría sopesar algunos indicios teóricos sobre la dimensionalidad del constructo y la precisión de la medida en pos de aproximarse a alcanzar el equilibrio deseado entre ellas.

A modo de recomendación e integrando los resultados del presente estudio con los aportes de otros investigadores (Kramp, 2006; Lee & Paek, 2014; Maydeu-Olivares et al., 2009) parece aconsejable recurrir a una escala Likert con más opciones si se puede asumir que el constructo presenta una dimensión teórica claramente dominante (por lo que sería esperable un adecuado ajuste) pero hay preocupación por la estimación de los niveles del rasgo porque, por ejemplo, se requiere que la prueba sea breve. Por otro lado, si se considera que el constructo es relativamente complejo a nivel teórico y se sospechan problemas para alcanzar un ajuste, sería conveniente recurrir a una menor cantidad de categorías. Si se supone que esto puede perjudicar a la precisión de la medida, se debería manipular otras características de la escala, como la cantidad de ítems que componen el test o la inclusión de ítems altamente discriminativos.

Uno de los aspectos que convendría seguir investigando en futuros estudios es por qué empeoraron las evidencias internas de validez en los formatos con mayor cantidad de categorías. Con más opciones de respuestas, la decisión del evaluado se complejiza ya que debe refinar la discriminación entre las categorías (Campbell, 1988). Sin embargo, con la complejidad de la decisión aumenta la probabilidad de aparición de heurísticas tendientes a simplificar el proceso cognitivo que demanda la tarea. Aun teniendo disponible muchas categorías, el sujeto podría emplear un número más limitado de opciones que utiliza como puntos de anclaje (Durán, Ocaña, Cañadas & Pérez Santa María, 2000; Weathers, Sharma & Niedrich, 2005). La variedad y cantidad de heurísticas que usen los sujetos podrían ser el resultado de factores tanto situacionales como disposicionales (estilos de respuesta). En este sentido, el aumento en la cantidad de categorías podría contribuir a la diversificación de las variables involucradas en la determinación de las respuestas de un individuo a un ítem o al test. Consecuentemente, parece razonable que se torne más difícil de satisfacer el supuesto de unidimensionalidad requerido por el MCP. Estudios cualitativos como los desarrollados por Kulas y Stachowski (2013), en donde se les solicita a un grupo de evaluados que reporten en voz alta el proceso que los llevó a elegir la respuesta al ítem, podrían dilucidar el grado en que podría ser sistematizado este fenómeno.

FINANCIAMIENTO

Esta investigación fue financiada con los subsidios de la Universidad de Buenos Aires UBACyT 2018 con Códigos 20020170100200BA y 20020170200001BA y de la Agencia Nacional de Promoción Científica y Tecnológica PICT-2017-3226.

CONFLICTO DE INTERESES

Los autores expresamos que no presentamos conflictos de interés al redactar el manuscrito.

REFERENCIAS

Abal, F. J. P., Auné, S. E., & Attorresi, H. F. (2014). Comparación del Modelo de Respuesta Graduada y la Teoría Clásica de Tests en una escala de confianza para la matemática. Summa Psicológica UST, 11(2), 101-113. doi: 10.18774/summa-vol11.num2-158.

Abal, F. J. P., Auné, S. E., Lozzia, G. S., & Attorresi, H. F. (2015). Modelización de una prueba de afecto hacia la matemática con la teoría de respuesta al ítem. Revista de Psicología UCA, 11(21), 23-34. Recuperado de http://uca.edu.ar/es/facultad-de-psicologia-y-psicopedagogia/revista-de-psicologia

Abal, F. J. P., Auné, S. E., Lozzia, G. S. & Attorresi, H. F. (2017). Funcionamiento de la categoría central en ítems de Confianza para la Matemática. Evaluar, 17(2), 18-31. Recuperado de https://revistas.unc.edu.ar/index.php/revaluar.

Abal, F. J. P, Lozzia, G. S., Auné, S. E. & Attorresi, H. F. (2017). El Modelo de Crédito Parcial aplicado a la escala Distorsión del Big Five Questionnaire. Actualidades en Psicología, 31 (122), 133-148. doi: 10.15517/ap.v31i122.23499.

Abal, F. J. P., Galibert, M. S., Aguerri, M. E., & Attorresi, H. F. (2014). Comparación de los modelos respuesta graduada y crédito parcial aplicados a una escala de utilidad de la matemática. Revista Argentina de Ciencias del Comportamiento, 6(3), 6-16. Recuperado de https://revistas.unc.edu.ar/index.php/racc/

Adelson, J. L., & McCoach, D. B. (2011). Development and psychometric properties of the Math and Me Survey: Measuring third through sixth graders' attitudes towards mathematics. Measurement and Evaluation in Counseling and Development, 44 (4), 225-247. doi: 10.1177/0748175611418522.

Adelson, J. L., & McCoach, D. B. (2010). Measuring the mathematical attitudes of elementary students: The effects of a 4-point or 5-point Likert-type scale. Educational and Psychological Measurement, 70 (5), 796-807. doi: 10.1177/0013164410366694

Alwin, D. F., Baumgartner, E. M. & Beattie, B. A. (2018). Number of Response Categories and Reliability in Attitude Measurement. Journal of Survey Statistics and Methodology, 6 (2), 212–239. doi: 10.1093/jssam/smx025

Andrich, D. (2016). Rasch Rating-Scale Model. En W. J. van der Linden (Ed.). Handbook of Item Response Theory, Volume 1: Models (pp. 75-94). Boca Raton: Chapman y Hall/CRC.

Ato, M., López. J. J., & Benavente. A. (2013). Un sistema de clasificación de los diseños de investigación en psicología. Anales de Psicología. 29 (3). 1038 - 1059. doi: 10.6018/analesps.29.3.178511.

Auzmendi, E. (1992). Las actitudes hacia la matemática-estadística en las enseñanzas medias y universitarias. Bilbao: Mensajero.

Bandura, A. (2006). Guide for constructing self-efficacy scales. In F. Pajares & T. Urdan (Eds.). Self-efficacy beliefs of adolescents, (Vol. 5., pp. 307-337). Greenwich, CT: Information Age Publishing.

Bazán, J., & Sotero, H. (1998). Una aplicación al estudio de actitudes hacia la matemática en la Unalm. Anales Científicos UNALM, 36, 60-72.

Bisquerra, R., & Pérez-Escoda, N. (2015). ¿Pueden las escalas Likert aumentar en sensibilidad? REIRE, Revista d’Innovació i Recerca en Educació, 8 (2), 129-147. doi: 10.1344/reire2015.8.2828

Campbell, D. J. (1988). Task complexity: A review and analysis. Academy of Management Review, 13, 40-52. doi: 10.5465/amr.1988.4306775.

Champney, H., & Marshall, H. (1939). Optimal refinement of the rating scale. Journal of Applied Psychology, 23, 323-331.

Coe, R. & Merino, C. (2003). Magnitud del efecto: Una guía para investigadores y usuarios. Revista de Psicología de la PUCP, 21 (1), 147-177. Recuperado de http://revistas.pucp.edu.pe/index.php/psicologia

Cox, E. P. (1980). The optimal number of response alternatives for a scale: A review. Journal of Marketing Research, 17 (4), 407-422. doi: 10.2307/3150495.

Culpepper, S. A. (2013). The reliability and precision of total scores and IRT estimates as a function of polytomous IRT parameters and latent trait distribution. Applied Psychological Measurement, 37 (3), 201-225. doi: 10.1177/0146621612470210

DeVellis, R. F. (2017). Scale development: Theory and application (4th Edition). Newbury Park, CA: Sage.

Diedenhofen, B. & Musch, J. (2015). cocor: A Comprehensive Solution for the Statistical Comparison of Correlations. PLoS ONE, 10 (4), e0121945. doi:10.1371/journal.pone.0121945.

DiStefano, C., Morgan, G. B. & Motl, R. W. (2012).An examination of personality characteristics related to acquiescence.Journal of applied measurement, 13(1), 41-56.

Domínguez-Lara, S. & Merino-Soto, C. (2015). ¿Por qué es importante reportar los intervalos de confianza del coeficiente alfa de Cronbach? Revista Latinoamericana de Ciencias Sociales, Niñez y Juventud, 13, 1326 - 1328.

Dunn, T. J., Baguley, T., & Brunsden, V. (2014). From alpha to omega: A practical solution to the pervasive problem of internal consistency estimation. British Journal of Psychology, 105 (3), 399–412. doi: 10.1111/bjop.12046

Durán, A, Ocaña, A. C., Cañadas, I. & Pérez Santamaría, F. J. (2000). Construcción de cuestionarios para encuestas: el problema de la familiaridad de las opciones de respuesta. Metodología de Encuestas, 2 (1) 27-60. Recuperado de http://casus.usal.es/pkp/index.php/MdE

Elosua, P. & Zumbo, B. D. (2008). Coeficientes de fiabilidad para escalas de respuesta categórica ordenada. Psicothema, 20 (4), 896-901.

Embretson, S. & Reise, S. (2000). Item Response Theory for Psychologists. Mahwah, NJ: Erlbaum Publishers.

Fennema, E., & Sherman, J. A. (1976). Fennema-Sherman Mathematics Attitudes Scales: Instruments designed to measure attitudes toward the learning of mathematics by females and males. Journal for Research in Mathematics Education, 7 (5), 324-326. doi: 10.2307/748467.

Finn, J. A., Ben-Porath, Y. S. & Tellegen, A. (2015). Dichotomous Versus Polytomous Response Options in Psychopathology Assessment: Method or Meaningful Variance? Psychological Assessment, 27 (1), 184-193. doi: 10.1037/pas0000044.

Gadermann, A. M., Guhn, M., & Zumbo, B. D. (2012). Estimating Ordinal Reliability for Likert-Type and Ordinal Item Response Data: A Conceptual, Empirical, and Practical Guide. Practical Assessment, Research & Evaluation, 17(3), 1-13.

Gempp, R., Denegri, M., Caprile, C., Cortés, L., Quesada, M. & Sepúlveda, J. (2006). Medición de la alfabetización económica en niños: oportunidades diagnósticas con el modelo de crédito parcial. Psykhe, 15 (1), 13-27. doi: 10.4067/S0718-22282006000100002.

George, D. & Mallery, M. (2016). IBM SPSS Statistics 23 Step by Step A Simple Guide and Reference (14th Edition). Boston, MA: Allyn and Bacon.

Ghasemi, A. & Zahedias, S. (2012). Normality Tests for Statistical Analysis: A Guide for Non-Statisticians. Int J Endocrinol Metab, 10 (2), 486–489. doi: 10.5812/ijem.3505.

González, V., & Espejo, B. (2003). Testing the middle response categories “Not sure”, “In between” and “?” in polytomous items. Psicothema, 15(2), 278-284.

González-Betanzos, F., Leenen, I., Lira-Mandujano, J. & Vega-Valero, Z. (2012). The Effect of the Number of Answer Choices on the Psychometric Properties of Stress Measurement in an Instrument Applied to Children. Evaluar, 12, 43 – 59.

Guilford, J. P. (1954). Psychometric methods (2nd ed.). New York: McGraw-Hill.

Hair, J. F., Black, W. C., Babin, B. J. & Anderson, R. E., (2009). Multivariate Data Analysis (7th edition). Upper Saddle River, NJ: Prentice Hall.

Hernández, A., Muñiz, J. & García-Cueto, E. (2000). Comportamiento del modelo de respuesta graduada en función del número de categorías de la escala. Psicothema, 12 (2), 288-291.

Jones, W. P. & Loe, S. A. (2013). Optimal Number of Questionnaire Response Categories: More May Not Be Better. SAGE. Open, 3, 1–10. doi: 10.1177/2158244013489691

Joshi, A., Kale, S., Chandel, S., & Pal, D. K. (2015). Likert -scale: Explored and explained. British Journal of Applied Science & Technology, 7 (4), 396-403. doi: 10.9734/BJAST/2015/14975

Kelley, K. (2007). Constructing confidence intervals for standardized effect sizes: Theory, application, and implementation. Journal of Statistical Software, 20 (8), 1–24. doi: 10.18637/jss.v020.i08

Kelley, K., & Pornprasertmanit, S. (2016). Confidence intervals for population reliability coefficients: Evaluation of methods, recommendations, and software for composite measures. Psychological Methods, 21, 69 – 92. doi:10.1037/a0040086

Kramp, U. (2006). Efecto del número de opciones de respuesta sobre las propiedades psicométricas de los cuestionarios de personalidad (Tesis doctoral, Universidad de Barcelona). Recuperada de http://www.tesisenred.net/bitstream/handle/10803/2535/ UKD_TESIS.pdf?sequence=1

Kulas, J. T., & Stachowski, A. A. (2013). Respondent rationale for neither agreeing nor disagreeing: Person and item contributors to middle category endorsement intent on Likert personality indicators. Journal of Research in Personality, 47 (4), 254–262. doi: 10.1016/j.jrp.2013.01.014

Lee, J. & Paek, I. (2014). In Search of the Optimal Number of Response Categories in a Rating Scale. Journal of Psychoeducational Assessment, 32 (7), 663–673. doi: 10.1177/0734282914522200.

Linacre, J. M. (2012). Winsteps® Rasch measurement computer program User's Guide. Beaverton, Oregon: Winsteps.com.

Lloret-Segura, S., Ferreres-Traver, A., Hernández-Baeza, A., & Tomás-Marco, I. (2014). El análisis factorial exploratorio de los ítems: una guía práctica, revisada y actualizada. Anales de Psicología, 30 (3), 1151-1169.

Lozano, L. M., García-Cueto, E. & Muñiz, J. (2008). Effect of the Number of Response Categories on the Reliability and Validity of Rating Scales. Methodology, 4 (2), 73–79. doi 10.1027/1614-2241.4.2.73.

MacDonald, K. (2018). A Review of the Literature: The Needs of Nontraditional Students in Postsecondary Education. Strategic Enrollment Management Quarterly, 5 (4), 159–164. doi:10.1002/sem3.20115

Martínez, O. J. (2008). Actitudes hacia la matemática. Sapiens. Revista Universitaria de Investigación, 9 (1), 237-256.

Masters, G. N. & Wright, B. D. (1997). The Partial Credit Model. En W. J. Van der Linden y R. K. Hambleton (Eds.). Handbook of Modern Item Response Theory, (pp. 101-121). New York: Springer.

Masters, G. N. (1982). A Rasch model for partial credit scoring. Psychometrika, 47, 149 - 174.

Masters, G. N. (2016). Partial Credit Model. En W. J. van der Linden (Ed.). Handbook of Item Response Theory, Volume 1: Models (pp. 109-126). Boca Raton: Chapman & Hall/CRC.

Matas, A. (2018). Diseño del formato de escalas tipo Likert: un estado de la cuestión. Revista Electrónica de Investigación Educativa, 20 (1), 38-47. doi: 10.24320/redie.2018 .20.1.1347

Matell, M. S. & Jacoby, J. (1971) Is there an optimal number of Likert scale items? Study I: Reliability and validity. Educational and Psychological Measurement, 31, 657-674.

Maydeu-Olivares, A., Kramp, U., García-Forero, C., Gallardo-Pujol, D. & Coffman, D. (2009). The effect of varying the number of response alternatives in rating scales: Experimental evidence from intra-individual effects. Behavior Research Methods, 41 (2), 295-308. doi:10.3758/BRM.41.2.295.

McLeod, D. & McLeod, S. (2002). Synthesis – Beliefs and Mathematics Education: Implications for Learning, Teaching and Research. En G. Leder, E. Pehkonen, & G. Törner (Eds.), Beliefs: A hidden variable in mathematics education? (pp. 115-126). Dordrecht: Kluwer Academic Publishers.

Morales, P.M. (2006). Medición de actitudes en Psicología y Educación. Madrid: Universidad Pontificia Comillas.

Muñiz, J., García-Cueto, E., & Lozano, L. M. (2005). Item format and the psychometric properties of the Eysenck Personality Questionnaire. Personality and Individual Differences, 38, 61-69. doi: 10.1016/j.paid.2004.03.021

Muthén, L. & Muthén, B. (2010). Mplus User’sGuide, 6thEdn. Los Angeles, CA: Muthén & Muthén.

Nunes, C. H. S. S., Primi, R., Nunes, M. F. O., Muniz, M., Cunha, T. F. & Couto, G. (2008). Teoria de Resposta ao Item para otimização de escalas tipo likert– um exemplo de aplicação. RIDEP, 25, 51 – 79.

Palacios, A., Arias, V., & Arias, B. (2014). Attitudes Towards Mathematics: Construction and Validation of a Measurement Instrument. Revista de Psicodidáctica, 19 (1), 67-91. doi: 10.1387/RevPsicodidact.8961.

Penfield, R. D. (2014). An NCME Instructional Module on Polytomous Item Response Theory Models. Educational Measurement: Issues and Practice, 33, 36-48. doi: 10.111/emip.12023

Peters, G. J. Y. (2014). The alpha and the omega of scale reliability and validity: Why and how to abandon Cronbach’s alpha and the route towards more comprehensive assessment of scale quality. European Health Psychologist, 16 (2), 56–69. Recuperado de http://www.ehps.net/ehp/index.php/contents.

Preston, C. C. & Colman, A. M. (2000). Optimal number of response categories in rating scales: Reliability, validity, discriminating power, and respondent preferences. Acta Psychologica, 104, 1-15. doi:10.1016/S0001-6918(99)00050-5.

Rasch, G. (1960). Probabilistic Models for Some Intelligence and Attainment Tests. Copenhague: The Danish Institute for Educational Research.
Rojas, A. J. & Pérez, C. (2001). Nuevos Modelos para la Medición de Actitudes. Valencia: Promolibro.

Samejima, F. (2016). Graded Response Model. En W. J. van der Linden (Ed.). Handbook of Item Response Theory, Volume 1: Models (pp. 95-108). Boca Raton: Chapman y Hall/CRC.

Sancerini, M. D., Meliá, J. L., & González-Romá, V. (1990). Formato de respuesta, fiabilidad y validez, en la medición del conflicto de rol. Psicológica, 11, 167-175.

Sancerni, M. D., Meliá, J. L. & González-Romá, V. (1990). Formato de respuesta, fiablidad y validez en la medición del conflicto de rol. Psicológica, 11, (2), 167-175.

Shea, T. S., Tennant, A. & Pallant, J. F. (2009). Rasch model analysis of the Depression, Anxiety and Stress Scales (DASS). BMC Psychiatry, 9 (1), 21. doi: 10.1186/1471-244X-9-21

Sijtsma, K. (2009). On the Use, the Misuse, and the Very Limited Usefulness of Cronbach’s Alpha. Psychometrika, 74 (1), 107–120.

Smith, A. B., Fallowfield, L. J., Stark, D. P., Velikova, G. & Jenkins, V. (2010). A Rasch and confirmatory factor analysis of the General Health Questionnaire (GHQ)-12. Health and Quality of Life Outcomes, 8 (1), 45. doi 10.1186/1477-7525-8-45

Symonds, P. M. (1924). On the Loss of Reliability in Ratings Due to Coarseness of the Scale. Journal of Experimental Psychology, 7 (6), 456-461. doi: 10.1037/h0074469

Tapia, M., & Marsh, G. E. (2004). An instrument to measure mathematics attitudes. Academic Exchange Quarterly, 8, 16-21.

Toland, M. D. & Usher, E. L. (2016). Assessing Mathematics Self-Efficacy: How Many Categories Do We Really Need? The Journal of Early Adolescence, 36, 932-960. doi: 10.1177/0272431615588952.

Vendramini, C., Silva, M. & Dias, A. (2009). Avaliação de atitudes de estudantes de psicologia via modelo de crédito parcial da TRI. Psico-USF, 14 (3), 287-298. doi: 10.1590/S1413-82712009000300005.

Wakita, T., Ueshima, N. & Noguchi, H. (2012). Psychological Distance Between Categories in the Likert Scale: Comparing Different Numbers of Options. Educational and Psychological Measurement, 72 (4): 533- 546. doi: 10.1177/0013164411431162

Weathers, D., Sharma, S. & Niedrich, R. W. (2005). The impact of the number of scale points, dispositional factors, and the status quo decision heuristic on scale reliability and response accuracy. Journal of Business Research, 58 (11), 1516-1524. doi: 10.1016/j.jbusres.2004.08.002

Weng, L.J. (2004). Impact of the number of response categories and anchor labels on coefficient alpha and test-retest reliability. Educational and Psychological Measurement, 64, 956-972. doi: 10.1177/0013164404268674

Wetzel, E. & Greiff, S. (2018). The world beyond rating scales. Why we should think more carefully about the response format in questionnaires. European Journal of Psychological Assessment, 34, 1-5. doi: 10.1027/1015-5759/a000469.

Willse, J. T. (2017). Polytomous Rasch Models in Counseling Assessment. Measurement and Evaluation in Counseling and Development, 50 (4), 248-255. doi: 10.1080/07481756.2017.1362656

Wright, B. D., Linacre, J. M., Gustafson, J. E., & Martin-Lof, P. (1994). Reasonable mean-square fit values. Rasch measurement transactions, 8 (3), 370. Recuperado de https://rasch.org/rmt/contents.htm

Zanini, D. S. & Peixoto, E. M. (2016). Social Support Scale (MOS-SSS): Analysis of the Psychometric Properties via Item Response Theory. Paidéia, 26 (65), 359-368. doi: 10.1590/1982-43272665201612

Zou, G. Y. (2007). Toward Using Confidence Intervals to Compare Correlations. Psychological Methods, 12 (4), 399–413. doi: 10.1037/1082-989X.12.4.399