Aaron Caycho Caja ^{1 *} y César Abraham Castilla Arias ²

¹ Universidad Privada del Norte, Perú.

² Universidad Nacional Federico Villarreal, Perú.

^* Correspondencia: aaronkaycho@gmail.com

Recibido: 07 de mayo de 2020
Revisado: 02 de agosto de 2020
Aceptado: 16 de agosto de 2020
Publicado Online: 17 de agosto de 2020

Caycho, A. & Castilla, C. (2020). Evaluación de un modelo bifactorial y propiedades psicométricas del FACES III en estudiantes peruanos. Interacciones, 6(2), e160. http://dx.doi.org/10.24016/2020.v6n2.160

ABSTRACT

Background: To analyze the internal structure of the Family Adaptability and Cohesion Evaluation Scales-FACES III by evaluating three tentative models. Method: Non-probability sampling of 306 Peruvian students of both sexes between 15 and 26 years of age. The structural properties and internal consistency of the Original, Bifactorial and One-dimensional models were studied in detail. Results: The bifactorial model has a better fit than the remaining models, but was discarded as it does not satisfy the criteria of the suggested evaluation indices. Likewise, difficulties are observed in the internal consistency of the Flexibility subscale except for the One-Dimensional Model. Conclusion: FACES III is an instrument with consistency and internal structure problems directly associated with the presence of the Flexibility subscale as reported in previous studies.

INTRODUCCIÓN

El modelo circumplejo de sistemas maritales y familia (Olson, Sprenkle y Russell, 1979) busca explicar la funcionalidad familiar y fue creado con la intención de cubrir la brecha entre la investigación, la teoría y la práctica. Asimismo, integra tres dimensiones: cohesión, flexibilidad y comunicación: la cohesión es el grado de unión emocional percibido por los sujetos que conforman la familia y la autonomía individual que experimentan sus miembros (Olson et al., 1979); flexibilidad es entendida como la magnitud de cambio de roles, reglas liderazgo que experimenta la familia (Olson et al., 1979); y comunicación indica los niveles saludables que permitirán el movimiento entre las dos dimensiones del modelo (Olson, 2000). Se añade que tanto la dimensión de flexibilidad y cohesión forman parte del modelo circumplejo inicial que facilita la explicación de 16 tipos de sistemas maritales y familiares (Olson et al., 1979).

Basados en el modelo circumplejo se creó la escala FACES I, una versión extensa de 111 ítems distribuidos en las dimensiones de Cohesión familiar y Adaptabilidad (Flexibilidad), las cuales evidenciaron un coeficiente alfa de 0.83 y 0.65 respectivamente (Bell, 1980). Posteriormente, con la finalidad de mejorar sus propiedades psicométricas y tener un instrumento más corto se creó el FACES II (Olson, Portner & Bell, 1982), el cual permitió desarrollar versiones abreviadas como el FACES 20Esp (Martínez-Pampliega, Iraurgi, Galindez & Sanz, 2006; Martínez-Pampliega, Iraurgi & Sanz, 2011). En este último, los autores investigaron una muestra de estudiantes españoles y plantearon un análisis factorial confirmatorio (AFC) jerárquico de segundo orden en el cual se asume la Cohesión y Adaptabilidad como factores ortogonales de primer orden y Funcionamiento Familiar como un constructo subyacente a la Cohesión y Adaptabilidad, pero de segundo orden (Martínez-Pampliega et al., 2011). Al respecto se menciona que los índices de ajuste del modelo jerárquico (CFI=97; GFI=95; SRMR=0.038; RMSEA=0,052) son favorables y las escalas de Cohesión y Adaptabilidad evidenciaron coeficientes alfa de consistencia interna de 0,82 y 0,79 para Cohesión y Adaptabilidad respectivamente.

No obstante, otros estudios y algunos problemas asociados a la ortogonalidad teórica de los factores del FACES II (Olson, 1986) dieron paso a la aparición del FACES III. Según Olson (2000) es con el FACES III, donde se crea la tercera dimensión llamada comunicación, la cual no está gráficamente incluida en el modelo. Otra de las finalidades de esta tercera versión fue tratar de que la correlación entre Cohesión y Adaptabilidad fuera lo más cercana a cero; lo cual se consiguió ya que se pasó del r= 0,65 del Faces II al r= 0,03 del FACES III y demostró la independencia de las dimensiones (Olson, 1986). Asimismo, en ese estudio fue replicada la estructura factorial de dos constructos subyacentes y se hallaron coeficientes de alfa de 0.62 en Adaptabilidad y 0.77 en Cohesión (Olson, 1986).

Posterior a su aparición, el FACES III ha generado diversas investigaciones asociadas a sus propiedades psicométricas encontrando aspectos singulares que se relatan a continuación. Por ejemplo, João, Martínez y Cervera (2002) estudiaron familias de niños en España y realizaron un AFC de cada subescala encontrando que Cohesión obtuvo una bondad de ajuste de X²/gl= 1.15, CCFI= .98, RMSR= 0.044, SRMSR= 0.042 RMSEA= 0.019, GFI, .983, AGFI= .971; mientras que la subescala de Adaptabilidad obtuvo coeficientes X²/gl= 2.48, CCFI= .91, RMSR= 0.12, SRMSR= 0.069, RMSEA= 0.055, GFI, .974, AGFI = .948, pero evidenció saturaciones factoriales < 0.30 entre los ítems “14”, “18” y “20”. Los coeficientes de consistencia interna indican un alfa de 0.72 para Cohesión y 0.68 en Adaptabilidad. El estudio (João, et al, 2002) destaca los problemas asociados a la consistencia interna de la escala de Adaptabilidad, ya presentes incluso en la versión original (Olson, 1986) del FACES III.

De manera similar, Ide, Dingmann, Cuevas y Meehan (2010) estudiaron dos muestras de adolescentes de dos condados de Norteamérica. Mediante el empleo de un Análisis de Componentes Principales con rotación Varimax encontraron dos factores subyacentes, sin embargo, estos evidenciaron problemas de bajas correlaciones ítem – total en Adaptabilidad. Asimismo, Ide et al., (2010) identificaron coeficientes alfa de 0.89 en la subescala de Cohesión y 0.70 en Adaptabilidad para el condado de Laramie. Los mismos coeficientes de confiabilidad se obtuvieron en el condado de Sheridan. No obstante, se esperaba obtener correlaciones bajas entre las subescalas por considerar a ambas ortogonales (Olson, 1985); sin embargo, se obtuvieron correlaciones significativas entre ellas de 0.48 y 0.42 para las dos muestras de los condados. El estudio culmina señalando los ítems problemáticos de Adaptabilidad así como las dificultades asociadas a su consistencia interna (Ide et al., 2010).

En América hispana, Schmidt, Barreyro y Maglio (2010) realizaron un AFC con una muestra de padres y adolescentes argentinos. Los autores plantearon un primer AFC considerando un factor general y hallaron que los índices fueron ineficaces para explicar los resultados de la covariancia observada (AGFI= 0.851; RMR= 0.102; CFI= 0.711; IFI= 0.713; RMSEA= 0.078). Luego hicieron un AFC con dos factores, pero el modelo mejoró insuficientemente (AGFI= 0.913; RMR= 0,085; CFI= 0.856; IFI= 0.857; RMSEA= 0.074). Dichos resultados llevaron a realizar otro AFC con tres factores, logrando que el modelo se ajuste mejor a los datos (AGFI=0.932; RMR=0.07; CFI=0.90; IFI=0.90; RMSEA=0.063). Asimismo, se señalan coeficientes alfa de 0.82 para Cohesión, 0.60 para “Flexibilidad 1” y 0.37 para “Flexibilidad 2” (Schmidt et al., 2010).

En Perú, Bazo-Álvarez et al. (2016) estudiaron las propiedades psicométricas del FACES III con 911 adolescentes y, mediante un análisis factorial exploratorio (AFE), encontraron los dos factores subyacentes hipotetizados. Asimismo, El AFC final de los autores mantiene la totalidad de los ítems e indica una bondad de ajuste favorable (X²/gl= 4.17, GFI= 0.96; ECVI= 0,87; NFI= 0.93; GFI= 0.97; RMSEA= 0.059); no obstante, solo fueron reportados los valores de la consistencia interna para el AFE (omega ≥ 0.70). Asimismo, Villarreal y Paz (2017) replicaron los dos factores subyacentes del FACES III mediante un AFE en una muestra de estudiantes peruanos. El AFC de Villarreal y Paz (2017) indica una bondad de ajuste favorable para Cohesión (X²/gl = 2.12, GFI=0.955; CFI=0,955; AGFI=0.982; RMSEA= 0.054) pero con problemas en el factor de Adaptabilidad (X²/gl = 2.89, GFI=0.947; CFI=0,588; AGFI=0.915; RMSEA=0.105), por lo cual solo procedieron a hallar la consistencia interna de la subescala de Cohesión (ω = .81). No obstante, concluyen señalando las propiedades psicométricas inadecuadas del FACES III y enfatizan los problemas hallados con la escala de Adaptabilidad.

En síntesis, del análisis realizado en el FACES III, si bien varios autores han procurado destacar las propiedades psicométricas de la escala, esta ha tenido problemas asociados a la consistencia de la escala de Flexibilidad (Bazo-Álvarez et al., 2016; João et al., 2002; Olson, 1986; Schmidt et al., 2010; Villarreal & Paz, 2009;) o problemas asociados a la estructura factorial del FACES III evidenciados en la cantidad de factores (Schmidt et al, 2010; Villarreal & Paz, 2009).

En ese sentido, se hace necesario estudiar si los resultados se inclinan a considerar el FACES III como una escala con propiedades psicométricas inadecuadas originadas por las dificultades halladas en la subescala de Flexibilidad; más aún si se toma en cuenta la necesidad de emplear instrumentos que evalúen el funcionamiento familiar en estudiantes peruanos de la forma más adecuada posible o incluso orientar los estudios hacia nuevas versiones como el FACES IV, desarrollado posteriormente.

MÉTODO

Participantes

Se empleó un estudio no probabilístico con 306 estudiantes de un centro preuniversitario de la Provincia Constitucional del Callao en Perú, con edades de entre 15 y 26 años (M= 17 años); de este total, 38.7% son de sexo femenino y el restante masculino; de los cuales un 58.7% menciona pertenecer a una familia nuclear, 11.1% a una familia monoparental, 23% a un tipo de familia extensa, 20% a una familia fusionada; y el 2% restante a otros casos. Asimismo, el 39.7% de las familias percibe mensualmente un sueldo mayor a los 450 dólares y el restante posee un sueldo menor a esta cantidad.

Instrumentos

Se empleó la Escala de Adaptabilidad y Cohesión Familiar - FACES III elaborada por Olson (1985) que contiene 20 ítems en formato Likert correspondientes a las dimensiones de Cohesión y Flexibilidad. Como fue mencionado previamente, esta escala fue adaptada en Perú por Bazo-Álvarez et al. (2016) quienes destacan sus propiedades psicométricas, aunque no reportaron los problemas de consistencia interna en el AFC del estudio. Villarreal y Paz (2017) también realizaron la validación del FACES III en muestra peruana, pero sus conclusiones destacan las desfavorables características del instrumento, en especial la subescala de Adaptabilidad.

Procedimiento

Se solicitaron los permisos respectivos a la dirección del centro preuniversitario para la aplicación del instrumento en mención junto con una ficha sociodemográfica. Posteriormente, se realizó la aplicación de la prueba en una única fecha, pero en cinco diferentes salones. Durante la aplicación del instrumento, se explicó a los participantes los fines de estudio así como también se les solicitó la autorización respectiva mediante un consentimiento informado el cual fue aceptado por la totalidad de los participantes. Al finalizar la aplicación del instrumento, se agradeció a los participantes al igual que a las autoridades del centro de estudios.

Análisis de datos

El análisis estadístico básicamente fue realizado a través del software estadístico R versión 3.5.2, library Lavaan. Asimismo, se implementa un modelo bifactorial en el cual existe un factor general que explica tanto los factores específicos ortogonales entre sí como a la totalidad de ítems correspondientes a este factor general. En este modelo los factores específicos son ortogonales ya que se asume que la varianza compartida de ambos se da por el factor general (Reise, 2012). Se añade que el análisis del modelo Bifactorial planteado fue contrastado a través de índices de evaluación mediante las hojas de cálculo propuestas por Dueber (2017), las cuales se fueron complementando con un formato virtual para el cálculo del coeficiente Omega (ω) de consistencia interna (Gouveia & Soares, 2015) y una hoja de Excel (Hammer, 2016) para el cálculo del coeficiente H de confiabilidad de constructo (Hancock, 2001).

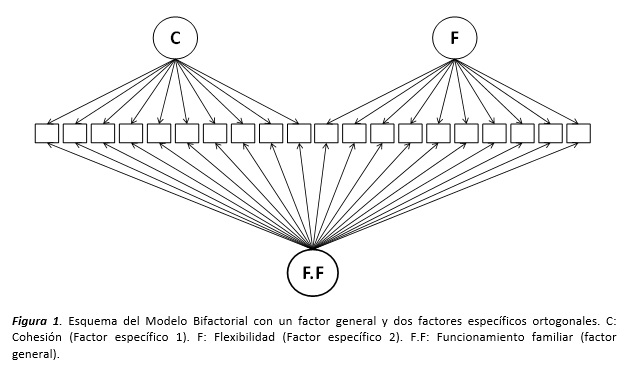
Luego de las consideraciones previas a la ejecución del AFC (Hair, Anderson & Black 1999), se realizó un AFC de la matriz de correlaciones policóricas debido al tipo de variable ordinal del FACES III (Freiberg, Stover, de la Iglesia & Fernández, 2013) para lo cual fue empleada la estimación por Mínimos Cuadrados Ponderados Robustos (WLSMV). Posteriormente, en vista de las investigaciones previas las cuales consideran el FACES III a partir de dos constructos subyacentes (Olson, 1985), fue planteado un Modelo Original en las mismas condiciones, no obstante, llamó la atención la presencia de una alta correlación entre los factores subyacentes; por lo cual fue sugerido un Modelo Bifactorial. Este tipo de modelo asume la presencia de un factor subyacente a los 20 ítems que conforman la escala total así como también la presencia de dos factores ortogonales subyacentes (Cohesión y Flexibilidad), los cuales cargan en los ítems que les corresponden teóricamente (figura 1).

Asimismo, se tomó especial atención en el planteamiento del modelo Bifactorial ya que este tipo de estudios solucionaría problemas teóricos asociados a los supuestos de ortogonalidad del FACES II y III señalados (Olson, 1985) y podría tener una explicación más parsimoniosa del Funcionamiento Familiar como constructo general y las dimensiones de Flexibilidad y Cohesión como constructos subyacentes, los cuales se asumirían completamente ortogonales de manera similar al estudio de Martínez-Pampliega et al. (2011). Adicionalmente, al sugerirse un modelo Bifactorial, también se consideró la presencia de un Modelo Unidimensional con la totalidad de los ítems, sobre todo con la intención de contrastarlo con el Modelo Bifactorial propuesto.
Se menciona que el ajuste de los modelos estudiados tomó como referencia índices de bondad pertinentes en este tipo de estudios: RMSEA ≤ 0.07, SRMR ≤ 0.08, CFI ≥ 0.92, TLI ≥ 0.92 (Hair, Black, Babin, & Anderson, 2014) y un Chi cuadrado normado 1 ≤ X²/gl ≤ 5 (Wu, 2013).

Seguidamente al análisis de la bondad de ajuste del modelo, se observó que el Modelo Bifactorial evidenciaba mejores índices de ajuste en comparación de los modelos Original y Unidimensional, lo cual permitiría afirmar su primacía respecto a los modelos planteados. Sin embargo, estudios previos (Rodríguez, Reise & Haviland, 2016a; Rodríguez, Reise & Haviland, 2016b) han considerado emplear índices de evaluación de la pertinencia de los modelos bifactoriales a través del cálculo de la varianza común explicada (ECV); la saturación factorial general, evaluada mediante el Omega jerárquico (ωH_g); el porcentaje de correlaciones no contaminadas (PUC); y el coeficiente H de confiabilidad de constructo. Al respecto, se ha procurado tomar como referencia los puntos de corte sugeridos (Rodríguez et al., 2016a) para los índices de evaluación (ωH_g > 0.70, ECV > 0.70, PUC > 0.70, H > 0.70).

De igual manera, se puso a prueba la consistencia interna de cada modelo mediante el cálculo del coeficiente Omega (ω) de las subescalas y el Omega (ω_t) de la escala esperándose que los modelos asuman valores mayores a 0,70 para ser considerados adecuados así como también fue empleado el coeficiente H de Hancock (2001) con un valor H> 0.80. Las propiedades psicométricas de los modelos planteados se complementan con el cálculo del monto promedio de la varianza (AVE), el cual brinda información respecto a la validez convergente y discriminante de cada modelo (Fornell & Larcker, 1981).

Aspectos éticos

El presente estudio contó con la aprobación de las áreas de Coordinación y Dirección de la institución. Asimismo, los participantes dieron su anuencia a la investigación mediante un consentimiento informado firmado voluntariamente. Se añade que se cumplieron con las normas éticas sugeridas en la Declaración de Helsinki de 1975.

RESULTADOS

Se realizaron análisis univariados y multivariados de los datos para procurar las mejores condiciones del AFC. En ese sentido, fueron evaluados 306 sujetos para superar la muestra mínima requerida (N ≥ 200) para la ejecución de un AFC. Los análisis univariados evidencian linealidad entre las variables de estudio y no se hallaron problemas de multicolinealidad o valores de asimetría o kurtosis mayores a 1.5. El análisis multivariado de los datos mediante la distancia D de Mahalanobis evidencia un único dato atípico que fue retirado por alejarse del centroide del total de las variables. Adicionalmente, el test de Mardia indica que los datos no poseen normalidad multivariada; no obstante, no se evidencian demasiados riesgos en continuar con el AFC (Hair, Anderson, Tatham & Black, 1999).

A partir de las investigaciones previas (Bazo-Álvarez et al., 2016; Ide et al., 2010; João, et al., 2002; Villarreal & Paz, 2017) se planteó un AFC con dos factores subyacentes (Modelo Original), los cuales mostraron un coeficiente de correlación entre los factores alto (0.79); sin embargo, anteriormente Bazo-Álvarez et al., (2016) ya habían obtenido valores similares (0.83) entre Cohesión y Flexibilidad, y con similar bondad de ajuste (AGFI = 0.96, X²/gl = 4.17, RMSEA = 0.059, GFI = 0.97) que el presente estudio. No obstante, las cargas factoriales en los ítems “5”, “6”, “14” y “20” son menores a 0.30, pero se mantuvieron en el modelo para mantener los supuestos teóricos del modelo (Olson, 1985).

Adicionalmente, si bien se han encontrado controversias referentes al empleo del análisis factorial de cada subescala por separado (Bazo-Álvarez et al., 2017; Copez & Domínguez, 2017), se ha considerado estudios previos (Bazo-Álvarez et al, 2016; Ide et al., 2010; Villarreal & Paz, 2017) que los han sugerido o empleado. En ese sentido, se creyó conveniente brindar información con fines estadísticos más que teóricos respecto a la bondad de ajuste de la subescala de Flexibilidad ya que esta evidenció problemas respecto a sus propiedades psicométricas (Bazo-Álvarez et al., 2016; Villarreal & Paz, 2017). Se menciona que al analizar únicamente esta subescala se mantienen las saturaciones factoriales bajas con los mismos ítems y la bondad de ajuste es deficiente (SRMR = 0.101, RMSEA = 0.118; CFI = 0.835; = GFI = 0.963; AGFI = 0.910; TLI = 0.788) y por debajo de los puntos de cortes asumidos por Bazo-Álvarez et al. (2016) y los considerados por los autores del presente estudio; pero no ocurre lo mismo cuando se realiza el AFC únicamente de la subescala de Cohesión ya que esta muestra un excelente ajuste (SRMR = 0.049, RMSEA = 0.037; CFI = 0.997; = GFI = 0.994; TLI = 0.996).

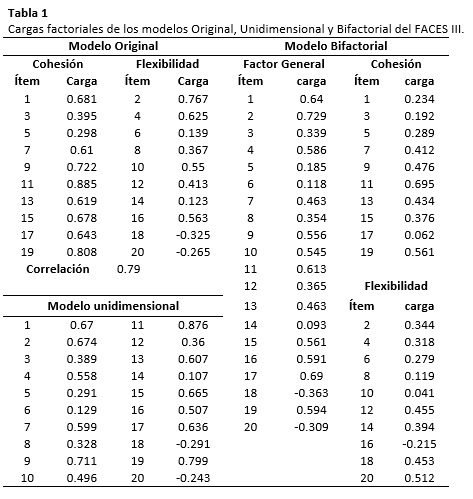
Volviendo nuevamente al análisis del AFC del Modelo Original, llamó la atención la alta correlación entre los factores de Cohesión y Flexibilidad. En estas circunstancias, la presencia de la alta correlación entre Cohesión y Flexibilidad y la evidencia previa de un factor general subyacente en el estudio del modelo jerárquico de segundo orden realizado por Martínez-Pampliega et al. (2011), respaldan el planteamiento de un modelo Bifactorial. Sin embargo, como este modelo Bifactorial no corresponde propiamente a las características que señalan Revelle y Zinbarg (2009) para un modelo unidimensional, se ha visto conveniente plantear un Modelo Unidimensional adicional de contraste. Se señala que el modelo Bifactorial muestra cargas factoriales > 0.30 en el factor general de Funcionamiento Familiar (F.F) a excepción de los ítems 5 y 6, mientras que en sus factores específicos se encuentran cargas < 0.30 en cuatro ítems de cada subescala. Asimismo el Modelo Unidimensional muestra ítems con cargas factoriales < 0.30 al igual que el Modelo Original. La tabla 1 muestra las cargas factoriales de los modelos planteados para el FACES III.

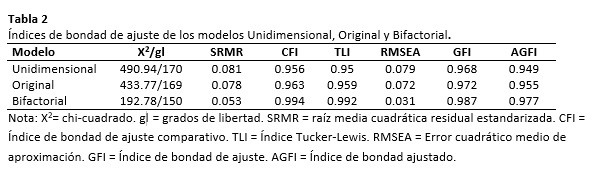
Si bien el Modelo Bifactorial muestra cargas factoriales bajas en varios ítems de los factores específicos, llama la atención que la bondad de ajuste del modelo Bifactorial supere largamente al Modelo Original y al Modelo Unidimensional y se muestre como un modelo que sin lugar a duda evidenciaría un buen ajuste. Asimismo, el Modelo Unidimensional no llega mostrar completamente mejores índices de ajuste que el Modelo Original propuesto; lo cual se indica en la tabla 2 que muestra la bondad de los modelos planteados.

A pesar de estos hallazgos, algunas investigaciones ya han señalado el mejor ajuste de los modelos bifactoriales (Cucina & Byle, 2017) en comparación a otros modelos. Sin embargo, últimamente se ha estado cuestionado el uso únicamente de la bondad de ajuste como criterio para la elección de un modelo Bifactorial sobre otros (Rodríguez et al., 2016a).

En este contexto, el Modelo Bifactorial fue analizado a través de los índices de evaluación sugeridos (Rodríguez, et al. 2016a), los cuales brindan mayores características psicométricas de los modelos bifactoriales. En ese sentido, el ωH_g aporta información respecto a la varianza debida a un factor general, lo cual apoyaría la unidimensional del modelo (Revelle & Zinbarg, 2009). En la misma línea, pero con ciertas diferencias respecto al ωH_g, el ECV (Sijitsma, 2009; Ten Berge & Socan, 2004) brinda información de la varianza común del total de los ítems respecto a una única dimensión (Rodríguez et al., 2016b). El ECV (S&E) (Stucky & Edelen, 2015) refleja la fuerza de un factor específico; y el ECV (NEW), la varianza explicada de los ítems en un factor especifico (Rodríguez et al., 2016a). Asimismo, el uso del ECV debe ir acompañado del empleo del PUC asociado a la proporción de la varianza del factor general en términos de covarianza (Rodríguez et al., 2016b). A partir de estos índices se evalúa propiamente si el modelo posee un factor general común a todos los ítems (Revelle & Zinbarg, 2009) y si no existe problemas en forzar datos multidimensionales a una medida esencialmente unidimensional, característica de un modelo bifactorial (Rodríguez et al., 2016b).

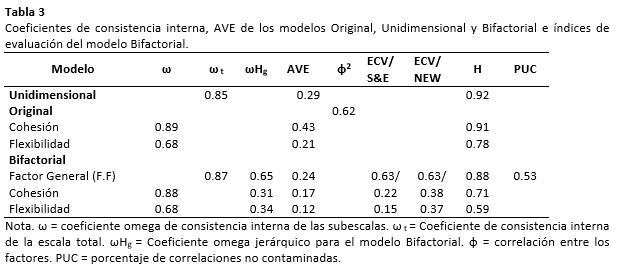
No obstante, los análisis de los índices de evaluación planteados evidencian que el modelo Bifactorial propuesto no cumple con ningún de los valores solicitados exceptuando únicamente el coeficiente H = 0.88 en el factor general F.F.; por lo cual se cuestiona seriamente el asumir únicamente la bondad de ajuste como único criterio para la elección de un modelo Bifactorial sobre otro tipo de modelos y se afirma el empleo de los índices de evaluación para el contraste de los modelos Bifactoriales.

Por otro lado, se menciona que la consistencia interna de los tres modelos planteados solo evidenció un coeficiente ω elevado en el Modelo Unidimensional (0.847) lo cual también se evidencia en un coeficiente H superior a 0.80. No sucede lo mismo en el modelo Original y Bifactorial que si bien muestran valores ω mayores a 0.80 para Cohesión tanto en el modelo Original y Bifactorial, muestra valores de 0.68 en la subescala de Flexibilidad en ambos modelos, los cuales son menores al punto de corte referencial de 0.70. No obstante, en algunos casos puede asumirse valores ligeramente menores (> 0.65), lo cual podría apoyar a la consistencia interna y favorecer a la validez del contenido del FACES III.

Finalmente, se obtuvo el AVE de los modelos planteados, sin embargo, los valores obtenidos no cumplen los criterios establecidos (Fornell & Larcker, 1981) para respaldar la validez discriminante de las subescalas del modelo Original y tampoco alcanzan el punto de corte esperado (> 0.50) para apoyar la validez interna convergente en los modelos Original, Unidimensional y Bifactorial.
La tabla 3 muestra los coeficientes de las propiedades psicométricas asociados a la confiabilidad, la validez de los modelos propuestos.

DISCUSIÓN

Luego de los análisis realizados, se muestran las evidencias psicométricas del FACES III en los modelos Unidimensional, Original y Bifactorial propuestos en el presente manuscrito. Respecto al modelo Original, se indica que inicialmente se planteó un AFC en las mismas condiciones que los estudios realizados en muestras peruanas (Bazo- Álvarez et al., 2016, Villarreal & Paz, 2017) quienes procuraron mantener la estructura factorial de dos factores subyacentes con la totalidad de sus ítems pares e impares respectivos a las subescalas de Flexibilidad para no alterar aspectos teóricos de la escala (Olson, 1985). Otros estudios también hallaron complicaciones similares asociadas a la consistencia interna en las subescalas de Flexibilidad y Cohesión (João, et al., 2002; Ide et al., 2010), pero procuraron mantener la totalidad de los ítems al igual que en la presente.

Como se mencionó, se puso a prueba un Modelo Original con la totalidad de los ítems distribuidos en dos subescalas, evidenciándose cargas factoriales menores a 0.30 en los ítems “5” de Cohesión y en los ítems “6”, “14” y “20” de Flexibilidad, lo cual concuerda con los hallazgos previos de Bazo-Álvarez et al. (2016) quienes también encontraron cargas factoriales menores a 0.30 en los ítems “5, “6”, “14” y 20”, y Villarreal y Paz (2017) quienes también hallaron saturaciones menores a 0.30 en los ítems “6”, “14” y “20” y otros más de la subescala de Flexibilidad, no obstante, se mantuvieron para no alterar el modelo teórico propuesto (Olson, 1985). Asimismo, a pesar de que la mayoría de índices de bondad de ajuste del modelo está dentro de los puntos de corte considerados (RMSEA ≤ 0.06, SRMR ≤ 0.08, CFI ≥ 0.90, TLI ≥ 0.90), el valor del RMSEA (0.072) supera el punto de corte sugerido (Hair et al., 2014) y genera inquietudes respecto al ajuste del modelo pero puede ser admitido como favorable (RMSEA ≤ 0.08) (MacCallum, Browne & Sugawara, 1996).

Además, si bien la subescala de Cohesión muestra solo un ítem con carga factorial menor a 0.30 y evidencia un coeficiente ω = 0.89, y H = 0.91, no sucede lo mismo en la subescala de Flexibilidad, la cual evidencia ítems con cargas factoriales bajas y además muestra un ω = 0.68 y H= 0.78, considerados bajos. En ese sentido, aunque los estudios realizados por Bazo-Álvarez et al. (2016) obtienen coeficientes de omega más altos para Flexibilidad (0.74), estos coeficientes corresponden al AFE ya que la confiabilidad de las subescalas en el AFC no fue reportada. Sin embargo, con las saturaciones factoriales del AFC del manuscrito de Bazo-Álvarez et al. (2016) se obtuvo un coeficiente omega (ω) 0.83 para Cohesión, pero de 0.55 para Flexibilidad, lo cual revela problemas de consistencia interna en esta subescala. Otros investigaciones (João, et al. 2002; Ide et al., 2010) también encuentran coeficientes ≤ 0.70 en esta subescala.

De La misma manera, Schmidt et al., (2010) hallaron dificultades en Flexibilidad; y, además, señalan problemas métricos ya señalados por Olson (1985), los cuales se asocian a la inicial construcción de la subescala y fue un motivo que conllevó a que se proponga el FACES IV (Schmidt, et al., 2010). Adicionalmente a estas cuestiones, Villarreal y Paz (2017) encontraron serios problemas relacionados a la estructura interna de Flexibilidad que incluso impidieron continuar con el análisis de la subescala ya que consideraron innecesario la obtención de los coeficientes de consistencia interna a causa de los contratiempos presentados respecto a la bondad de ajuste observados.

De manera paralela al estudio, se realizó un AFC de la subescala de Flexibilidad y Cohesión por separado, evidenciándose bajos índices de bondad de ajuste en Flexibilidad (SRMR= 0.101, RMSEA= 0.118; CFI= 0.835; GFI= 0.963) en contraste a los excelentes indicadores de la subescala de Cohesión; lo cual apoyaría a los cuestionamientos realizados hacia esta subescala. Probablemente la reespecificación de los ítems problemáticos de Flexibilidad mejoraría la bondad de ajuste del Modelo Original, no obstante, exigiría la modificación de aspectos teóricos del FACES III que tendrían que ser concedidos con finalidades más estadísticas que teóricas, lo cual ya ha sido observado previamente por Bazo-Álvarez et al. (2016).

Por otra parte, el Modelo Unidimensional propuesto evidencia cargas factoriales menores a 0.30 en los mismos ítems del modelo Original (ítems “5, “6”, “14” y 20”). Asimismo, la bondad de ajuste observada (GFI= 0.96, RMSEA= 0.079, NFI= 0.934, AGFI= 0.949, SRMR= 0.081), muestran valores debajo de los puntos exigidos para el RMSEA y el SRMR; lo cual en este caso ya es un indicador de problemas de bondad de ajuste. Sin embargo, la consistencia interna del Modelo Unidimensional muestra un ω = 0.85 y H = 0.92 que apoyan a la consistencia de la escala tomada en su conjunto como medición del Funcionamiento Familiar. En resumen, el Modelo Unidimensional posee favorable consistencia interna, pero evidencia problemas asociados a sus índices de bondad ajuste, los cuales también son inferiores a los del Modelo Original. Ciertamente los ítems de Flexibilidad perjudican al modelo; por lo cual sería comprensible el análisis únicamente de la subescala de Cohesión, tal y como Villarreal y Paz (2017) realizaron.

Respecto al Modelo Original, este viene mostrando complicaciones asociadas a cargas factoriales bajas en los mismos ítems que el Modelo Unidimensional, sobre todo en la subescala de Flexibilidad. En este contexto, el análisis del Modelo Bifactorial podría haber solucionado un problema al ser considerado más coherente con la propuesta de la construcción del FACES III que asume sus dos factores subyacentes ortogonales de primer grado, pero que en el AFC de Bazo-Álvarez et al. (2016) evidenciaron una correlación elevada (0.83), además de mantener la presencia del factor general F.F. común a la totalidad de los ítems. En una primera revisión, las ventajas señaladas se veían respaldadas por los índices de ajuste del Modelo Bifactorial (RMSEA = 0.031, SRMR = 0.053, CFI= 0.99, TLI = 0.99) que cumplen los puntos de corte más exigentes considerados en el presente estudio. Asimismo, la consistencia interna de la subescala de Cohesión evidenció un ω > 0.80; la subescala de Flexibilidad, un ω del mismo valor que el modelo Original (0.68); y el factor general de Funcionamiento Familiar obtuvo un ω = 0.87 incluso más alto que el obtenido en el Modelo Unidimensional. En otras palabras, mantendría las propiedades psicométricas más adecuadas, además sus características guardarían relación a la propuesta teórica de Olson (1985). No obstante, al analizar las características del modelo Bifactorial, (unidimensionalidad, varianza debida a un factor general, la varianza común del total y la proporción de la varianza del factor general) los índices de evaluación del modelo Bifactorial no respaldan estos supuestos ya que sus valores se encuentran por debajo de lo esperado para considerar al modelo esencialmente unidimensional.

Otro aspecto considerado importante fue procurar fidelidad al modelo teórico asociado al FACES III, no obstante, el Modelo Unidimensional dejó una inquietud ya que es respaldado por los valores de los coeficientes ω y H, además su bondad de ajuste es casi cercana a la del Modelo Original. Probablemente el mantener los supuestos teóricos asociados a la subescala de Flexibilidad genera los problemas de bondad de ajuste que evidencia el FACES III, los cuales ya han sido señalados por Schmidt et al. (2010). En ese sentido, el realizar modificaciones en la subescala de Flexibilidad alteraría aspectos teóricos del modelo. Incluso, se podría pensar en una única dimensión con la totalidad de los ítems, la cual sería en este caso Funcionamiento familiar; no obstante el problema sería que se estaría dejando de lado la subescala de Flexibilidad y se alteraría la teoría del modelo circumplejo de Olson (2000), el cual considera el Funcionamiento Familiar a partir de sus dos subescalas de las que se obtienen las facetas del modelo teórico.

No obstante, entre los modelos propuestos, el Modelo Original seguiría siendo el más cercano a los supuestos teóricos iniciales de Olson (1985) y, además, mantendría características más acordes a las validaciones en muestras peruanas similares a la presente (Bazo-Álvarez et al., 2016; Villarreal & Paz, 2017); sin embargo, se tiene que indicar que al asumir criterios estrictos, la bondad de ajuste y la consistencia interna de este modelo evidenciaron dificultades, sobre todo en la subescala de Flexibilidad. Adicionalmente, el empleo del AVE (Fornell & Larcker, 1981) tampoco respalda la validez convergente de las escalas generales o subescalas y lo mismo ocurre en torno a la validez discriminante de las subescalas de los Modelos Bifactorial y Original.

Por otro lado, si bien la muestra de estudiantes preuniversitarios postulantes a una universidad nacional comparten muchas semejanzas con los estudiantes de educación secundaria de otros estudios (Bazo-Álvarez et al., 2016; Villarreal & Paz, 2017), probablemente se encuentren sometidos a otro tipo de exigencias familiares relacionadas al proceso de postulación, las cuales pueden estar influyendo en su percepción respecto a su familia. También se señala que el presente estudio emplea métodos no probabilísticos de muestreo, lo cual es una limitación al igual que el número de muestra empleado (N = 306), sobre todo si se quiere realizar comparaciones exhaustivas con otros estudios (Bazo-Álvarez et al., 2016; Villarreal & Paz, 2017).

Para finalizar, la forma original del FACES III evidenció problemas de consistencia interna asociados a la subescala de Flexibilidad, cargas factoriales bajas en varios de sus ítems y pésima bondad de ajuste cuando es realizado un AFC solo de esta subescala. Tampoco se evidenció que el FACES III posea el respaldo suficiente para apoyar su validez convergente y discriminante. En ese sentido, se sugiere realizar mayores investigaciones que se adicionen a los hallazgos previos (Villarreal & Paz, 2017) y los presentes respecto a las propiedades psicométricas del FACES III que se han mostrado desfavorables, pero pueden llevar a dirigir la atención a otras versiones de este como el FACES IV. Respecto al Modelo Bifactorial, se señala que el empleo de los índices de evaluación permitió obtener características psicométricas más exhaustivas que la bondad de ajuste usualmente empleada en el estudio de los modelos de este tipo.

ORCID

Aaron Caycho Caja https://orcid.org/0000-0003-1478-8954

César Abraham Castilla Arias https://orcid.org/0000-0003-1539-1107

AGRADECIMIENTOS

Los autores agradecen los permisos brindados por la Coordinación del centro preuniversitario para la ejecución del estudio.

CONFLICTO DE INTERESES

Los autores declaran no tener ningún conflicto de intereses.

FINANCIAMIENTO

La presente investigación fue autofinanciada.

REFERENCIAS

Bazo-Álvarez, J.C., Bazo-Álvarez, O.A., Águila, J., Peralta, F., Mormontoy, W., & Bennett, I.M. (2016). Propiedades psicométricas de la escala de funcionalidad familiar faces-III: un estudio en adolescentes peruanos. Rev Peru Med Exp Salud Pública, 33(3), 462-70. https://doi.org/10.17843/rpmesp.2016.333.2299

Bazo-Álvarez, J.C., Bazo-Álvarez, O.A., Águila, J., Peralta, F., Mormontoy, W., & Bennett, I.M. (2017). El modelo circumplejo tridimensional (3-D): sobre las mediciones no-curvilíneas del FACES-III. Rev Peru Med Exp Salud Publica, 34(1), 152-153. https://doi.org/10.17843/rpmesp.2017.341.2782

Bell, R.Q. (1980). Parant/adolescent relationship in families with runaways: Interaction types and circumplex model. (Tesis Doctoral).University of Minnesota.

Copez, A., & Domínguez, S.A. (2017). ¿Es necesario un análisis completo del perfil del FACES-III? Rev Peru Med Exp Salud Publica, 34(1), 151-152. https://doi.org/10.17843/rpmesp.2017.341.2781

Cucina, J., & Byle, K. (2017). Article The Bifactor Model Fits Better Than the Higher-Order Model in More Than 90% of Comparisons for Mental Abilities Test Batteries. J. Intell, 5 (27), 1-21. https://doi.org/10.3390/jintelligence5030027

Dueber, D. M. (2017). Bifactor Indices Calculator: A Microsoft Excel-based tool to calculate various indices relevant to bifactor CFA models. https://doi.org/10.13023/edp.tool.01

Fornell, C., & Larcker, D. (1981). Evaluating structural equation models with unobservable variables and measurement error. Journal of Marketing Research, 18(1), 39-50. https://doi.org/10.1177/002224378101800104

Freiberg, H., Stover, J., de la Iglesia, G., & Fernández, M. (2013). Correlaciones Policóricas y tetracóricas en estudios factoriales exploratorios y confirmatorios. Ciencias Psicológicas, 7(2), 151-164. Disponible en: http://www.scielo.edu.uy/scielo.php?script=sci_arttext&pid=S168842212013000200005&lng=es&tlng=es

Gouveia, V.V., & Soares, A.K.S (2015). Calculadora de validade de construto (CVC). João Pessoa, PB: BNCS/Universidade Federal da Paraíba. Disponible en: http://akssoares.com/psicometria/calculadora-vme-e-cc

Hair, J., Anderson, R., Tatham, R., & Black, W. (1999). Análisis multivariante. 5a Ed. Madrid, España: Prentice Hall.

Hair, J., Black, W., Babin, B., & Anderson, R. (2014). Multivariate data analysis. Seventh Edition. Edinburgh Gate, United Kingdom: Pearson.

Hammer, J. H. (2016). Construct Replicability Calculator: A Microsoft Excel-based tool to calculate the Hancock and Mueller (2001) H index [software de cálculo]. Disponible en: http://drjosephhammer.com

Hancock, G. R. (2001). Effect size, power, and sample size determination for structured means modeling and MIMIC approaches to betweengroups hypothesis testing of means on a single latent construct. Psychometrika, 66, 373–388. https://doi.org/10.1007/BF02294440

Ide, B., Dingmann, C., Cuevas, E., & Meehan, M. (2010). Psychometric Testing of the FACES III with Rural Adolescents. Journal of Family Social Work, 13, 410–419. https://doi.org/10.1080/10522150903513993

MacCallum, R. C., Browne, M. W., & Sugawara, H. M. (1996). Power analysis and determination of sample size for covariance structure modeling. Psychol. Methods, 1, 130–149. https://doi.org/10.1037/1082-989X.1.2.130

João, M., Martínez, P., & Cervera-Enguix, S. (2002) Confirmatory Factor Analysis, Reliability, and Validity of a Spanish Version of FACES III. The American Journal of Family Therapy, 30 (5), 439-449. https://doi.org/10.1080/01926180260296332

Martínez-Pampliega, A., Iraugi, I., & Sanz, M. (2011). Validez estructural del FACES 20-Esp: versión española de 20 ítems de la escala de evaluación de la cohesión y adaptabilidad familiar. RIDEP. 2011; 29 (1), 147–65. Disponible en: http://www.aidep.org/03_ridep/R29/r29art8.pdf

Olson, D.H., Sprenkle, D.H., & Russell, C.S. (1979), Circumplex Model of Marital and Family Systems: I. Cohesion and Adaptability Dimensions, Family Types, and Clinical Applications. Family Process, 18, 3-28. https://doi.org/10.1111/j.1545-5300.1979.00003.x

Olson, D.H., Portner, J., & Bell, R. (1982). FACES II: Family adaptability and cohesion evaluation scales. Minnesota: Family Social Science, University of Minnesota.

Olson, D.H. (1985). FACES III: Family Social Science. Minnesota: University of Minnesota.

Olson, D. H. (1986). Circumplex model VII: Validation studies and FACES III. Family Process, 25(3), 337–351. https://doi.org/10.1111/j.1545-5300.1986.00337.x

Olson, D.H. (2000). Circumplex Model of Marital and Family Systems. Journal of Family Therapy, 22 (2), 144-167. https://doi.org/10.1111/1467-6427.00144

Revelle, W., & Zinbarg, R.E. (2009). Coefficients Alpha, Beta, Omega, and the GLB: Comments on Sijtsma. Psychometrika, 74(1), 145-154. https://doi.org/10.1007/s11336-008-9102-z

Reise, S.P. (2012). The rediscovery of bifactor measurement models. Multivariate Behavioral Research, 47(5), 667-696. doi:10.1080/00273171.2012.715555

Rodriguez, A., Reise, S. P., & Haviland, M. G. (2016a). Applying bifactor statistical indices in the evaluation of psychological measures. Journal of Personality Assessment, 98(3), 223-237. https://doi.org/10.1080/00223891.2015.1089249

Rodriguez, A., Reise, S. P., & Haviland, M. G. (2016b). Evaluating Bifactor Models: Calculating and Interpreting Statistical Indices. Psychological Methods, 21(2), 137–150. https://doi.org/10.1037/met0000045

Schmidt, V., Barreyro, J.P., & Maglio, A.L. (2010). Escala de evaluación del funcionamiento familiar FACES III: ¿Modelo de dos o tres factores? Escritos de Psicología, 3(2), 30-36. Disponible en: http://www.redalyc.org/articulo.oa?id=271019811003

Sijtsma, K. (2009). On the use, misuse, and the very limited usefulness of Cronbach”s alpha. Psychometrika, 74(1), 107-120. https://doi.org/10.1007/S11336-008-9101-0

Stucky, B. D., & Edelen, M. O. (2015). Using hierarchical IRT models to create unidimensional measures from multidimensional data. In S. P. Reise & D. A. Revicki (Eds.), Handbook of item response theory modeling: Applications to typical performance assessment, (pp. 183-206). New York: Routledge.

Ten-Berge, J. M., & Socan, G. (2004). The greatest lower bound to the reliability of a test and the hypothesis of unidimensionality. Psychometrika, 69, 613 - 625. https://doi.org/10.1007/BF02289858

Villarreal-Zegarra, D., & Paz-Jesús, A. (2017). Cohesión, adaptabilidad y composición familiar en adolescentes del Callao, Perú. Propósitos y Representaciones, 5(2), 21 - 64. https://doi.org/10.20511/pyr2017.v5n2.158

Wu M. L. (2013). Questionnaire Statistical Analysis Practice-SPSS Operation and Application. Chongqing: Chongqing University Press.